Rekenliniaal | mechanische analoge computer

Basisbegrippen

In zijn meest eenvoudige vorm gebruikt de rekenliniaal twee logaritmische schalen om snel te kunnen vermenigvuldigen en delen. Deze veel voorkomende bewerkingen kunnen tijdrovend en foutgevoelig zijn wanneer ze op papier worden uitgevoerd. Complexere rekenlinialen maken andere berekeningen mogelijk, zoals vierkantswortels, exponentiëlen, logaritmen en goniometrische functies.

Wiskundige berekeningen worden uitgevoerd door een merkteken op de verschuifbare centrale strook uit te lijnen met een merkteken op een van de vaste stroken. De relatieve positie van andere markeringen kan dan worden bekeken. Getallen die op één lijn staan met de merktekens geven bij benadering de waarde van het product, het quotiënt of een ander berekend resultaat.

De gebruiker bepaalt de plaats van de decimale punt in het resultaat op basis van een mentale schatting. Wetenschappelijke notatie wordt gebruikt om de decimale punt te volgen in meer formele berekeningen. Optellen en aftrekken in een berekening gebeurt meestal mentaal of op papier, niet op de rekenliniaal.

De meeste rekenlinialen hebben drie lineaire stroken van dezelfde lengte. De stroken zijn parallel opgesteld en vergrendeld, zodat de middelste strook in de lengte kan worden bewogen ten opzichte van de andere twee. De buitenste twee stroken liggen vast, zodat hun relatieve posities niet veranderen.

Sommige rekenlinialen ("duplex" modellen) hebben schalen aan beide zijden van de duimstok en de glijstrip, andere aan één zijde van de buitenste strips en beide zijden van de glijstrip, weer andere slechts aan één zijde ("simplex" regels). Een schuifcursor met een verticale uitlijningslijn wordt gebruikt om overeenkomstige punten te vinden op schalen die niet naast elkaar liggen of, bij duplex modellen, zich aan de andere kant van de duimstok bevinden. De cursor kan ook een tussenresultaat registreren op een van de schalen.

 
Cursor op een rekenliniaal  

Een rekenliniaal gebruiken voor de berekening

Vermenigvuldiging

Een logaritme zet de bewerkingen vermenigvuldiging en deling om in optellen en aftrekken volgens de regels log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} en log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Door de bovenste schaal naar rechts te verplaatsen met een afstand van log ( x ) {{displaystyle \log(x)} , door het begin van de bovenste schaal te laten samenvallen met het label x {{displaystyle x} aan de onderkant, wordt elk getal y {{displaystyle y} , op positie log ( y ) {\displaystyle \log(y)} op de bovenste schaal, met het getal op positie log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} op de onderste schaal. Omdat log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} , geeft deze positie op de onderste schaal x y {\displaystyle xy}. het product van x en y . Om bijvoorbeeld 3 × 2 (op een rekenmachine weergegeven als 3*2) te berekenen, wordt de 1 op de bovenste schaal verplaatst naar de 2 op de onderste schaal. Het antwoord, 6, wordt afgelezen van de onderste schaal waar 3 op de bovenste schaal staat. In het algemeen wordt de 1 op de bovenste schaal verplaatst naar een factor aan de onderkant, en het antwoord wordt van de onderkant afgelezen waar de andere factor aan de bovenkant staat.

Bewerkingen kunnen "buiten de schaal vallen"; het diagram hierboven laat bijvoorbeeld zien dat de rekenliniaal de 7 op de bovenste schaal niet boven een getal op de onderste schaal heeft geplaatst, en dus geen antwoord geeft voor 2×7. In dergelijke gevallen kan de gebruiker de bovenste schaal naar links schuiven tot de rechter index op één lijn ligt met de 2, zodat hij effectief met 0,2 vermenigvuldigt in plaats van met 2, zoals in de afbeelding hieronder:

Hier moet de gebruiker van de rekenliniaal eraan denken de decimale punt op de juiste manier aan te passen om het uiteindelijke antwoord te corrigeren. We wilden 2×7 vinden, maar in plaats daarvan hebben we 0,2×7=1,4 berekend. Het echte antwoord is dus niet 1,4 maar 14. De schuif resetten is niet de enige manier om vermenigvuldigingen te verwerken die leiden tot resultaten buiten de schaal, zoals 2×7; er zijn ook andere methoden:

• (1) Gebruik de dubbeldekkerschalen A en B.
• (2) Gebruik de gevouwen schalen. In dit voorbeeld zet u de linker 1 van C tegenover de 2 van D. Verplaats de cursor naar 7 op CF, en lees het resultaat af van DF.
• (3) Gebruik de omgekeerde CI-schaal. Plaats de 7 op de CI-schaal boven de 2 op de D-schaal, en lees vervolgens het resultaat af van de D-schaal, onder de 1 op de CI-schaal. Aangezien de 1 op twee plaatsen op de CI-schaal voorkomt, zal één ervan altijd op schaal zijn.
• (4) Gebruik zowel de omgekeerde CI-schaal als de C-schaal. Zet de 2 van CI op één lijn met de 1 van D, en lees het resultaat van D af, onder de 7 op de C-schaal.

Methode 1 is gemakkelijk te begrijpen, maar gaat ten koste van de nauwkeurigheid. Methode 3 heeft het voordeel dat er slechts twee schalen nodig zijn.

Afdeling

De onderstaande afbeelding toont de berekening van 5,5/2. De 2 op de bovenste schaal ligt boven de 5,5 op de onderste schaal. De 1 op de bovenste schaal ligt boven het quotiënt, 2,75. Er is meer dan één methode om te delen, maar de hier gepresenteerde methode heeft het voordeel dat het eindresultaat niet buiten de schaal kan vallen, omdat men de keuze heeft om de 1 aan beide uiteinden te gebruiken.

Andere verrichtingen

Naast de logaritmische schalen hebben sommige rekenlinialen nog andere wiskundige functies gecodeerd op andere hulpschalen. De meest populaire zijn goniometrische, meestal sinus en tangens, gewone logaritme (log10) (voor het nemen van de log van een waarde op een vermenigvuldigingsschaal), natuurlijke logaritme (ln) en exponentiële (e^x ) schalen. Sommige regels bevatten een Pythagoraschaal, om zijden van driehoeken te berekenen, en een schaal om cirkels te berekenen. Andere hebben schalen voor het berekenen van hyperbolische functies. Bij lineaire regels zijn de schalen en hun etikettering in hoge mate gestandaardiseerd, waarbij variatie meestal alleen voorkomt in termen van welke schalen zijn opgenomen en in welke volgorde:

A, B	logaritmische schalen van twee decennia, gebruikt voor het vinden van vierkantswortels en kwadraten van getallen
C, D	logaritmische schalen van één decennium
K	logaritmische schaal van drie decaden, gebruikt voor het vinden van kubiekwortels en kubussen van getallen
CF, DF	"gevouwen" versies van de C- en D-schalen die beginnen bij π in plaats van bij eenheid; deze zijn handig in twee gevallen. Ten eerste, wanneer de gebruiker vermoedt dat een product dicht bij 10 zal liggen, maar niet zeker weet of het iets minder of iets meer dan 10 zal zijn, vermijden de gevouwen schalen de mogelijkheid om van de schaal af te wijken. Ten tweede, door het begin π te maken in plaats van de vierkantswortel van 10, wordt het vermenigvuldigen of delen door π (zoals gebruikelijk in wetenschappelijke en technische formules) vereenvoudigd.
CI, DI, DIF	"omgekeerde" schalen, die van rechts naar links lopen, gebruikt om 1/x-stappen te vereenvoudigen
S	gebruikt voor het vinden van sinussen en cosinussen op de D-schaal
T	gebruikt voor het vinden van raaklijnen en cotangens op de D- en DI-schaal.
ST, SRT	gebruikt voor sinus en tangens van kleine hoeken en omrekening van graden naar radialen
L	een lineaire schaal die samen met de C- en D-schalen wordt gebruikt voor het vinden van logaritmen en machten van 10 in basis-10
LLn	een reeks log-logschalen, gebruikt voor het vinden van logaritmen en exponentiëlen van getallen
Ln	een lineaire schaal, gebruikt samen met de C- en D-schalen voor het vinden van natuurlijke (basis e) logaritmen en e x {{x}}.

 

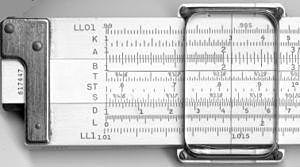
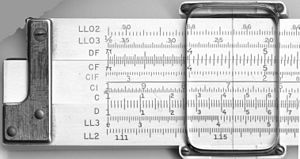
De schalen op de voor- en achterkant van een K&E 4081-3 rekenliniaal.

De binaire schuifregel die in 1931 door Gilson werd vervaardigd, had een optel- en aftrekfunctie die beperkt was tot breuken.

Wortels en krachten

Er zijn schalen met één decade (C en D), twee decaden (A en B) en drie decaden (K). Om x 2 te berekenen {{2}} bijvoorbeeld, plaatst u x op de D-schaal en leest u het kwadraat ervan af op de A-schaal. Door dit proces om te keren kunnen vierkantswortels worden gevonden, en evenzo voor de machten 3, 1/3, 2/3 en 3/2. Voorzichtigheid is geboden wanneer de basis, x, op meer dan één plaats op de schaal voorkomt. Er zijn bijvoorbeeld twee negens op schaal A; om de vierkantswortel van negen te vinden, gebruikt u de eerste; de tweede geeft de vierkantswortel van 90.

Voor x y {{y}} problemen gebruikt u de LL-schalen. Wanneer er meerdere LL-schalen zijn, gebruikt u degene met x erop. Lijn eerst de meest linkse 1 op de C-schaal uit met x op de LL-schaal. Zoek dan y op de C-schaal en ga naar beneden naar de LL-schaal met x erop. Die schaal geeft het antwoord aan. Als y "buiten de schaal valt", zoek dan x y / 2 {displaystyle x^{y/2}} en kwadrateer het met behulp van de A- en B-schalen zoals hierboven beschreven.

Trigonometrie

De S-, T- en ST-schalen worden gebruikt voor goniometrische functies en veelvouden van goniometrische functies, voor hoeken in graden. Bij veel rekenlinialen zijn de S-, T- en ST-schalen gemarkeerd met graden en minuten. Zogenaamde decitrig modellen gebruiken in plaats daarvan decimale fracties van graden.

Logaritmen en exponentiëlen

Basis-10 logaritmen en exponentiëlen worden gevonden met de L-schaal, die lineair is. Sommige rekenlinialen hebben een Ln-schaal, die voor basis e is.

De Ln-schaal werd in 1958 uitgevonden door Stephen B. Cohen, een student uit de 11e klas. De oorspronkelijke bedoeling was dat de gebruiker een exponent x (in het bereik van 0 tot 2,3) kon kiezen op de Ln-schaal en e^x kon aflezen op de C (of D) schaal en e^–x op de CI (of DI) schaal. Pickett, Inc. kreeg de exclusieve rechten op de schaal. Later creëerde de uitvinder een reeks "merktekens" op de Ln-schaal om het bereik uit te breiden tot voorbij de grens van 2,3, maar Pickett heeft deze merktekens nooit op zijn rekenlinialen aangebracht.

Optellen en aftrekken

Schuifregels worden gewoonlijk niet gebruikt voor optellen en aftrekken, maar het is toch mogelijk om dit te doen met behulp van twee verschillende technieken.

De eerste methode voor optellen en aftrekken op de C en D (of een vergelijkbare schaal) vereist dat het probleem wordt omgezet in een deling. Voor optellen is het quotiënt van de twee variabelen plus één keer de deler gelijk aan hun som:

x + y = ( x y + 1 ) y {displaystyle x+y=links({frac {x}{y}}+1rechts)y}

Voor aftrekken is het quotiënt van de twee variabelen min één keer de deler gelijk aan hun verschil:

x - y = ( x y - 1 ) y {displaystyle x-y=linker({frac {x}{y}}-1rechts)y}

Deze methode is vergelijkbaar met de optel-/aftrektechniek die wordt gebruikt voor snelle elektronische schakelingen met het logaritmische getallensysteem in gespecialiseerde computertoepassingen zoals de Gravity Pipe (GRAPE) supercomputer en verborgen Markov-modellen.

De tweede methode maakt gebruik van een glijdende lineaire L-schaal die op sommige modellen beschikbaar is. Optellen en aftrekken worden uitgevoerd door de cursor naar links (voor aftrekken) of naar rechts (voor optellen) te schuiven en vervolgens de schuif terug te brengen naar 0 om het resultaat af te lezen.

 

Fysiek ontwerp

Standaard lineaire regels

De lengte van de rekenliniaal wordt aangegeven in termen van de nominale lengte van de schalen. De schalen van de meest voorkomende "10 inch" modellen zijn in werkelijkheid 25 cm lang, omdat ze gemaakt zijn volgens metrische normen, hoewel sommige rekenlinialen iets langere schalen hebben om de manipulatie te vereenvoudigen wanneer een resultaat te hoog uitvalt. Zakregels zijn meestal 5 inch. Modellen van een paar meter lang werden verkocht om in klaslokalen te worden opgehangen voor onderwijsdoeleinden. [1]

Gewoonlijk markeren de verdelingen een schaal met een precisie van twee significante cijfers, en de gebruiker schat het derde cijfer. Sommige hoogwaardige rekenlinialen hebben vergrotende cursors die de markeringen beter zichtbaar maken. Dergelijke cursors kunnen de nauwkeurigheid van de aflezing verdubbelen, zodat een rekenliniaal van 10 inch net zo goed werkt als een rekenliniaal van 20 inch.

Er zijn verschillende andere gemakken ontwikkeld. Trigonometrische schalen zijn soms dubbel gelabeld, in zwart en rood, met complementaire hoeken, de zogenaamde "Darmstadt" stijl. Duplex rekenlinialen dupliceren vaak enkele schalen op de achterkant. Schalen worden vaak "gesplitst" om een hogere nauwkeurigheid te verkrijgen.

Gespecialiseerde rekenlinialen werden uitgevonden voor verschillende vormen van techniek, handel en bankieren. Deze hadden vaak veel voorkomende berekeningen rechtstreeks uitgedrukt in speciale schalen, bijvoorbeeld berekeningen voor leningen, optimale aankoophoeveelheden of bepaalde technische vergelijkingen. Het bedrijf Fisher Controls verspreidde bijvoorbeeld een aangepaste rekenliniaal, aangepast aan het oplossen van de vergelijkingen voor het selecteren van de juiste maat van industriële stroomregelkleppen.

Ronde rekenlinialen

Ringvormige rekenlinialen zijn er in twee basistypen, één met twee cursors (links), en één met een beweegbare schijf en één cursor (rechts). De versies met twee kruisdraden voeren vermenigvuldigingen en delingen uit door een vaste hoek tussen de kruisdraden aan te houden terwijl ze rond de schijf worden gedraaid. De versie met één cursor werkt meer als de standaard rekenliniaal door de juiste uitlijning van de schalen.

Het fundamentele voordeel van een cirkelvormige rekenliniaal is dat de langste afmeting van het gereedschap met een factor van ongeveer 3 (d.w.z. met π) werd verminderd. Bijvoorbeeld, de buitenste schaal van een 10 cm cirkelvormige rekenliniaal zou een maximale precisie hebben die gelijk is aan die van een 30 cm gewone rekenliniaal. Cirkelvormige rekenlinialen elimineren ook "off-scale" berekeningen, omdat de schalen ontworpen zijn om "rond te wikkelen"; ze hoeven nooit opnieuw georiënteerd te worden wanneer de resultaten in de buurt van 1,0 komen - de regel is altijd op schaal. Voor niet-cyclische niet-spiraalvormige schalen zoals S, T en LL's wordt de lengte van de schaal echter ingekort om ruimte te maken voor de eindmarges.

Cirkelvormige rekenlinialen zijn mechanisch robuuster en bewegen soepeler, maar de nauwkeurigheid van de schaaluitlijning is gevoelig voor de centrering van een centraal draaipunt; een minieme afwijking van 0,1 mm van het draaipunt kan in het ergste geval een uitlijningsfout van 0,2 mm opleveren. Het draaipunt voorkomt echter krassen op de wijzerplaat en de cursors. De meest nauwkeurige schalen bevinden zich op de buitenste ringen. In plaats van "gedeelde" schalen, gebruiken hoogwaardige linialen spiraalvormige schalen voor complexere bewerkingen zoals log-of-log schalen. Een premium duimstok van acht inch had een 50-inch spiraalvormige log-log schaal.

De belangrijkste nadelen van cirkelvormige rekenlinialen zijn de moeilijkheid om figuren langs een draaiende schijf te vinden, en het beperkte aantal schalen. Een ander nadeel van cirkelvormige rekenlinialen is dat minder belangrijke schalen dichter bij het midden liggen, en een lagere nauwkeurigheid hebben. De meeste leerlingen leerden het gebruik van rekenlinialen op de lineaire rekenlinialen, en vonden geen reden om over te stappen.

Een rekenliniaal die wereldwijd nog dagelijks wordt gebruikt is de E6B. Dit is een cirkelvormige rekenliniaal die in de jaren 1930 voor het eerst werd gemaakt voor piloten van vliegtuigen om hen te helpen bij de dead reckoning. Met behulp van schalen op het frame helpt hij ook bij diverse taken zoals het omrekenen van tijd, afstand, snelheid en temperatuur, kompasfouten en het berekenen van brandstofverbruik. De zogenaamde "gebedsmolen" is nog steeds verkrijgbaar in vliegwinkels en wordt nog steeds veel gebruikt. Hoewel GPS het gebruik van dead reckoning voor luchtvaartnavigatie heeft verminderd, en handheld rekenmachines veel van de functies ervan hebben overgenomen, wordt de E6B nog steeds veel gebruikt als primair of back-up apparaat, en de meeste vliegscholen eisen dat hun studenten het in zekere mate beheersen.

In 1952 introduceerde het Zwitserse horlogebedrijf Breitling een pilotenpolshorloge met een geïntegreerde ronde rekenliniaal die gespecialiseerd was in vluchtberekeningen: de Breitling Navitimer. De Navitimer rekenliniaal, door Breitling een "navigatiecomputer" genoemd, bevatte functies voor luchtsnelheid, klimtijd/daaltijd, vliegtijd, afstand en brandstofverbruik, evenals functies voor het omrekenen van kilometer-nautische mijlen en gallon-liter brandstofhoeveelheid.

Materialen

Schuifregels werden traditioneel gemaakt van hardhout, zoals mahonie of buxus, met cursors van glas en metaal. Ten minste één precisie-instrument was van staal.

In 1895 begon een Japanse firma, Hemmi, rekenlinialen te maken van bamboe, dat als voordeel had dat het vormvast, sterk en natuurlijk zelfsmerend was. Deze rekenlinialen van bamboe werden in september 1933 in Zweden geïntroduceerd [2], en waarschijnlijk iets eerder in Duitsland. De schalen waren gemaakt van celluloid of plastic. Latere rekenlinialen werden gemaakt van plastic, of aluminium beschilderd met plastic. Latere schuifregels waren van acryl of polycarbonaat die op Teflon lagers schoven.

Bij alle hoogwaardige rekenlinialen werden de cijfers en schalen gegraveerd en vervolgens gevuld met verf of andere hars. Geschilderde of bedrukte rekenlinialen werden als inferieur beschouwd omdat de markeringen konden slijten. Niettemin maakte Pickett, waarschijnlijk Amerika's meest succesvolle fabrikant van rekenlinialen, alle gedrukte schalen. Hoogwaardige rekenlinialen waren voorzien van slimme sluitingen zodat de duimstok niet per ongeluk uit elkaar zou vallen, en stootranden om de schalen en de cursor te beschermen tegen wrijving op tafelbladen. De aanbevolen reinigingsmethode voor gegraveerde markeringen is licht schrobben met staalwol. Voor geverfde rekenlinialen, en de zwakkeren van hart, gebruikt u verdunde ruitenreiniger en een zachte doek.

 
Breitling Navitimer polshorloge met ronde rekenliniaal  


Een eenvoudige cirkelvormige rekenliniaal, gemaakt door Concise Co., Ltd., Tokio, Japan, met alleen inverse, vierkante en kubusvormige schalen. Op de achterkant staat een handige lijst met 38 metrische/imperiale conversiefactoren.  


Pickett ronde rekenliniaal met twee cursors. (4,25 in./10,9 cm diameter) De achterkant heeft een extra schaalverdeling en een cursor.  

Geschiedenis

De rekenliniaal werd uitgevonden rond 1620-1630, kort na de publicatie door John Napier van het begrip logaritme. Edmund Gunter uit Oxford ontwikkelde een rekentoestel met één logaritmische schaal, waarmee, met aanvullende meetinstrumenten, kon worden vermenigvuldigd en gedeeld. De eerste beschrijving van deze schaal werd in 1624 in Parijs gepubliceerd door Edmund Wingate (ca. 1593 - 1656), een Engelse wiskundige, in een boek getiteld "L'usage de la reigle de proportion en l'arithmetique & geometrie". Het boek bevat een dubbele schaal, met aan de ene kant een logaritmische schaal en aan de andere kant een schaal in tabelvorm. In 1630 vond William Oughtred uit Cambridge een ronde rekenliniaal uit, en in 1632 combineerde hij twee Gunter-regels, die met de handen bij elkaar werden gehouden, tot een apparaat dat herkenbaar is als de moderne rekenliniaal. Net als zijn tijdgenoot in Cambridge, Isaac Newton, onderwees Oughtred zijn ideeën privé aan zijn studenten, maar vertraagde hij de publicatie ervan, en net als Newton raakte hij verwikkeld in een heftige controverse over voorrang, met zijn voormalige leerling Richard Delamain en de eerdere claims van Wingate. Oughtreds ideeën werden pas openbaar gemaakt in publicaties van zijn leerling William Forster in 1632 en 1653.

In 1677 creëerde Henry Coggeshall een duimstok van twee voet voor houtmeting, de Coggeshall rekenliniaal. Zijn ontwerp en het gebruik van het gereedschap gaven de rekenliniaal een doel buiten het wiskundig onderzoek.

In 1722 introduceerde Warner de twee- en drie-decade schalen, en in 1755 voegde Everard een omgekeerde schaal toe; een rekenliniaal die al deze schalen bevat wordt gewoonlijk een "polyphase" regel genoemd.

In 1815 vond Peter Roget de logaritmische rekenliniaal uit, die een schaal bevatte waarop de logaritme van de logaritme werd weergegeven. Hierdoor kon de gebruiker direct berekeningen uitvoeren met wortels en exponenten. Dit was vooral nuttig voor breuken.

Moderne vorm

De modernere vorm werd in 1859 gecreëerd door de Franse artillerieluitenant Amédée Mannheim, "die het geluk had dat zijn duimstok werd gemaakt door een firma met nationale reputatie en dat hij werd overgenomen door de Franse artillerie". Rond die tijd, toen techniek een erkende beroepsactiviteit werd, werden rekenlinialen in Europa algemeen gebruikt. Zij werden pas algemeen in de Verenigde Staten in 1881, toen Edwin Thacher er een cilindervormige duimstok introduceerde. De duplex duimstok werd uitgevonden door William Cox in 1891, en werd geproduceerd door Keuffel and Esser Co. uit New York.

Astronomisch werk vereiste ook fijne berekeningen, en in het Duitsland van de 19e eeuw werd op een sterrenwacht een stalen rekenliniaal van ongeveer 2 meter lang gebruikt. Er was een microscoop op bevestigd, waardoor de nauwkeurigheid zes decimalen bedroeg.

In de Tweede Wereldoorlog gebruikten bombardiers en navigators die snelle berekeningen nodig hadden vaak gespecialiseerde rekenlinialen. Een afdeling van de Amerikaanse marine ontwierp een generiek rekenliniaal "chassis" met een aluminium behuizing en plastic cursor waarin celluloid kaarten (aan beide zijden bedrukt) konden worden geplaatst voor speciale berekeningen. Het proces werd uitgevonden om het bereik, het brandstofverbruik en de hoogte voor vliegtuigen te berekenen, en werd vervolgens aangepast voor vele andere doeleinden.

In de jaren 1950 en 1960 was de rekenliniaal het symbool van het beroep van ingenieur (op dezelfde manier als de stethoscoop het medische beroep symboliseert). De Duitse raketgeleerde Wernher von Braun nam twee Nestler rekenlinialen uit de jaren 1930 mee toen hij na de Tweede Wereldoorlog naar de VS verhuisde om te werken aan het Amerikaanse ruimtevaartprogramma. Zijn hele leven lang gebruikte hij geen andere zakrekenmachines; rekenlinialen dienden hem uitstekend voor het maken van snelle schattingen van raketontwerpparameters en andere cijfers. Aluminium rekenlinialen van het merk Pickett gingen mee op vijf Apollo ruimtemissies, waaronder naar de maan, volgens reclame op Pickett's N600 rekenlinialen [3].

Sommige studenten en ingenieurs droegen rekenlinialen van tien inch in riemholsters, en zelfs tot halverwege de jaren zeventig was dit een normaal beeld op campussen. Studenten konden ook een duimstok van tien of twintig inch bewaren voor precisiewerk thuis of op kantoor, terwijl ze een duimstok van vijf inch in hun zak bij zich hadden.

In 2004 bedachten onderwijsonderzoekers David B. Sher en Dean C. Nataro een nieuw type rekenliniaal gebaseerd op prosthaphaeresis, een algoritme voor het snel berekenen van producten dat dateert van voor de logaritmen. Er was echter weinig praktische interesse om er een te bouwen, behalve het eerste prototype. [4] Archived 2005-05-10 at the Wayback Machine

Daling

Het belang van de rekenliniaal begon af te nemen toen elektronische computers, een nieuw maar zeer schaars middel in de jaren 1950, in de jaren 1960 algemeen beschikbaar werden voor technische werknemers. De introductie van Fortran in 1957 maakte computers praktisch voor het oplossen van wiskundige problemen van bescheiden omvang. IBM introduceerde een reeks beter betaalbare computers, de IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965), gericht op de wetenschappelijke en technische markt. John Kemeny's BASIC programmeertaal (1964) maakte het voor studenten gemakkelijk om computers te gebruiken. De DEC PDP-8 minicomputer werd geïntroduceerd in 1965.

Computers veranderden ook de aard van het rekenen. Bij rekenlinialen lag de nadruk op het bewerken van de algebra om uitdrukkingen in de meest berekenbare vorm te krijgen. Gebruikers van rekenlinialen benaderden of lieten kleine termen weg om de berekening te vereenvoudigen. Met Fortran konden ingewikkelde formules uit tekstboeken worden ingetypt zonder de moeite van herformulering. Numerieke integratie was vaak gemakkelijker dan het zoeken naar gesloten oplossingen voor moeilijke problemen. De jonge ingenieur die om computertijd vroeg om een probleem op te lossen dat met een paar vegen op de rekenliniaal had kunnen worden opgelost, werd een humoristisch cliché. Veel computercentra hadden een ingelijste rekenliniaal aan de muur hangen met de opmerking "In geval van nood, breek glas".

Een andere stap naar de vervanging van rekenlinialen door elektronica was de ontwikkeling van elektronische rekenmachines voor wetenschappelijk en technisch gebruik. De eerste was de Wang Laboratories LOCI-2, geïntroduceerd in 1965, die logaritmen gebruikte voor vermenigvuldiging en deling, en de Hewlett-Packard HP-9100, geïntroduceerd in 1968. De HP-9100 had goniometrische functies (sin, cos, tan) naast exponentiëlen en logaritmen. Hij gebruikte het CORDIC-algoritme (coordinate rotation digital computer), waarmee goniometrische functies kunnen worden berekend met alleen verschuivings- en optelbewerkingen. Deze methode vergemakkelijkte de ontwikkeling van steeds kleinere wetenschappelijke rekenmachines.

De laatste nagel aan de doodskist van de rekenliniaal was de lancering van wetenschappelijke rekenmachines op zakformaat, waarvan de HP-35 van Hewlett-Packard uit 1972 de eerste was. Deze rekenmachines werden bekend als "rekenlinialen" omdat ze de meeste of alle functies van een rekenliniaal konden uitvoeren. Met een prijs van enkele honderden dollars werd zelfs dit als duur beschouwd voor de meeste studenten. Terwijl professionele rekenlinialen ook vrij duur konden zijn, verkochten drogisterijen vaak plastic basismodellen voor minder dan 20 dollar. Maar tegen 1975 konden elektronische rekenmachines met vier functies gekocht worden voor minder dan 50 dollar. In 1976 bood de TI-30 een wetenschappelijke rekenmachine voor minder dan $25. Na deze periode droogde de markt voor rekenlinialen snel op omdat kleine wetenschappelijke rekenmachines betaalbaar werden.

 
TI-30  


Ingenieur die een rekenliniaal gebruikt. Let op de mechanische rekenmachine op de achtergrond.  


William Oughtred (1575-1660), uitvinder van de cirkelvormige rekenliniaal  

Voordelen

• Een rekenliniaal heeft de neiging de misvatting van "valse precisie" en significantie te matigen. De typische nauwkeurigheid waarover een gebruiker van een rekenliniaal beschikt, is ongeveer drie plaatsen nauwkeurig. Dit komt goed overeen met de meeste gegevens die beschikbaar zijn voor invoer in technische formules. Wanneer een moderne zakrekenmachine wordt gebruikt, kan de precisie worden weergegeven tot zeven of meer decimalen, terwijl de resultaten in werkelijkheid nooit nauwkeuriger kunnen zijn dan de beschikbare invoergegevens.
• Een rekenliniaal vereist een voortdurende schatting van de orde van grootte van de resultaten. Op een rekenliniaal geeft 1,5 × 30 (wat gelijk is aan 45) hetzelfde resultaat als 1.500.000 × 0,03 (wat gelijk is aan 45.000). Het is aan de ingenieur om voortdurend de redelijkheid van de resultaten vast te stellen, iets wat verloren kan gaan wanneer getallen achteloos in een computerprogramma of een rekenmachine worden ingevoerd.
• Wanneer een reeks vermenigvuldigingen of delingen door hetzelfde getal wordt uitgevoerd, kan het antwoord vaak worden bepaald door slechts een blik op de rekenliniaal te werpen zonder enige manipulatie. Dit kan bijzonder nuttig zijn bij het berekenen van percentages, bijvoorbeeld voor testscores, of bij het vergelijken van prijzen, bijvoorbeeld in dollars per kilogram. Meerdere snelheid-tijd-afstand berekeningen kunnen met een rekenliniaal hands-free in één oogopslag worden uitgevoerd.
• Een rekenliniaal is niet afhankelijk van elektriciteit.
• Een rekenliniaal is een gemakkelijk na te maken technologie. Van een gegeven voorbeeld van een rekenliniaal kunnen er meer worden gemaakt door een bekwaam ambachtsman uit rudimentaire materialen met behulp van niet-industriële processen.
• Schuifregels zijn in hoge mate gestandaardiseerd, dus u hoeft niets opnieuw te leren als u op een andere regel overschakelt.
• Rekenlinialen zijn veelzijdig, en kunnen worden bediend in situaties en omgevingen waar een menselijke gebruiker minder goed ter been is (bijvoorbeeld omdat hij beschermende handschoenen nodig heeft). Omgekeerd kan een rekenmachine in dergelijke situaties moeilijk te bedienen zijn - het is onwaarschijnlijk dat een rekenliniaal tot een soortgelijke fout leidt als het per ongeluk indrukken van de verkeerde knop op een rekenmachine.
• Rekenlinialen kunnen worden gemaakt van karton of papier. Veel gratis kaarten of gespecialiseerde rekenmachines van karton zijn eigenlijk gespecialiseerde lineaire of ronde rekenlinialen.

Een voordeel van het gebruik van een rekenliniaal samen met een elektronische rekenmachine is dat een belangrijke berekening kan worden gecontroleerd door deze op beide uit te voeren; omdat de twee instrumenten zo verschillend zijn, is er weinig kans om twee keer dezelfde fout te maken.

 

Nadelen

• Fouten kunnen het gevolg zijn van mechanische onnauwkeurigheid.
• Berekeningen met de rekenliniaal zijn van beperkte precisie vanwege hun analoge in- en uitgangen. Omgekeerd hebben zelfs bescheiden moderne rekenmachines, vanwege de discrete numerieke invoer en de elektronische bewerkingen met drijvende komma, uitvoerresoluties van ten minste zes significante cijfers.

 

Gerelateerde pagina's

• Abacus
• Logaritme