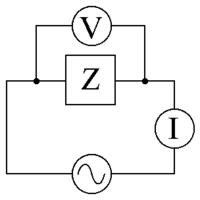
Impedantie

Elektrische impedantie is de hoeveelheid weerstand die een schakeling biedt aan stroom- of spanningsverandering.

De twee belangrijkste manieren om een impedantie te schrijven zijn: (zie de 2e figuur, "complex impedantievlak")

met de weerstand "R" (reëel deel) en de reactie "X" (denkbeeldig deel), bijvoorbeeld Z = 1 + 1 j {\playstyle Z=1+1j} $Z=1+1j$
met een grootte en een fase (de grootte van Z) $\left\vert Z\right\vert$ en de hoek van ∠. $\angle \theta$ ), bijvoorbeeld Z = 1.4 ∠ 45 ∘ {\playstyle Z=1.4 \\\ca 45^{circ }} $Z=1.4\angle 45^{\circ }$ (1,4 ohm bij 45 graden)

De Impedantie en de weerstand lijken sterk op elkaar:

In het geval van een weerstand is een weerstand bestand tegen elke stroom die erdoorheen gaat. Hoe hoger de weerstand, hoe hoger de spanning die nodig is om een bepaalde stroom te bereiken. De formule is:

V = R ∗ I {\playstyle V=R*I} $V=R*I$ , waarbij V de spanning is, R de weerstand, en I de stroom.

In het geval van impedantie is een inductor bestand tegen veranderingen in de stroom en de condensator tegen veranderingen in de spanning.

Het belangrijkste verschil tussen weerstand en impedantie is het woord "verandering", de snelheid van de verandering heeft invloed op de impedantie. Meestal wordt de "verandering" uitgedrukt als een frequentie, het aantal keren per seconde dat de stroom of de spanning van richting verandert. De formules zijn:

Voor de inductor: Z = j 2 π f L {\playstyle Z=j2\pi fL,} $Z=j2\pi fL\,$

Voor de condensator: Z = 1 j 2 π f C {\\frac {1}{j2\pi fC}} $Z={\frac {1}{j2\pi fC}}$

Waar Z het symbool voor de impedantie is, is j het denkbeeldige getal. ${\sqrt {-1}}$ ... $\pi$ is de constante pi, f is de frequentie, L is de inductie en C is de capaciteit. De eenheden voor de weerstand en de impedantie zijn hetzelfde, de ohm met het symbool Ω {displaystyle \Omega } $\Omega$ (kapitaal omega).

Zoals de bovenstaande formules aangeven, varieert de impedantie afhankelijk van de frequentie, bijvoorbeeld bij nul Hertz, of DC, de impedantie van de inductor is nul, hetzelfde als een kortsluiting, en de impedantie van de condensator is oneindig, hetzelfde als een open-circuit. De meeste signalen zijn de som van vele sinusgolven bij verschillende frequenties (zie de fouriertransformatie voor meer details), en elk van hen heeft een andere impedantie.

Net als de weerstand, hoe hoger de impedantie, hoe hoger de spanning die nodig is om een bepaalde stroom te bereiken. De formule is:

V = Z ∗ I {\playstyle V=Z*I} $V=Z*I$ , waarbij V de spanning is, Z de impedantie, en I de stroom.

Op het fysieke niveau, het vereenvoudigen van veel dingen:

de weerstand wordt veroorzaakt door de botsingen van de elektronen met de atomen in de weerstanden.
de impedantie in een condensator wordt veroorzaakt door het ontstaan van een elektrisch veld.
de impedantie in een inductor wordt veroorzaakt door het ontstaan van een magnetisch veld.

Een belangrijk verschil tussen de weerstand en de impedantie is dat een weerstand energie verdrijft, het wordt heet, maar een inductor en een condensator slaan de energie op en kunnen die energie weer teruggeven aan de bron als hij omlaag gaat.

Als de impedantie van de bron, de kabel en de belasting niet allemaal gelijk zijn, dan wordt een fractie van het signaal teruggekaatst naar de bron, waardoor stroom wordt verspild en er interferentie ontstaat. De verhouding van de reflectie kan worden berekend met:

Γ = Z L - Z S Z L + Z S {\\\\Gamma ={Z_{L}-Z_{S} \an over Z_{L}+Z_{S}} $\Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}$ waar Γ \\\\\\Gamma } $\Gamma$ (kapitaal gamma) is de reflectiecoëfficiënt, Z S $Z_{S}$ is de impedantie van de bron, Z L $Z_{L}$ is de impedantie van de belasting.

Elk medium dat een golf kan hebben heeft een golfimpedantie, zelfs lege ruimte (licht is een elektromagnetische golf en het kan in de ruimte reizen) heeft een impedantie van ongeveer 377 Ω. $\Omega$ .

Een grafische voorstelling van het complexe impedantievlak

Een AC-voeding met een spanning V die een scriptaanstijl V gebruikt... $\scriptstyle V$ ...over een impedantie Z, in de vorm van een script, Z... $\scriptstyle Z$ $\scriptstyle I$ ...met een huidige I{\\\\\\\\\\\\\\\\\\

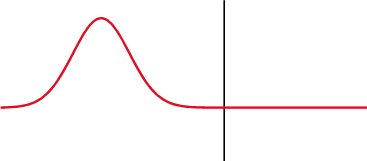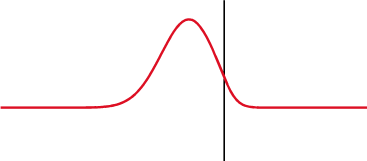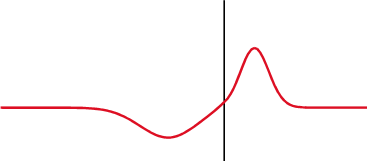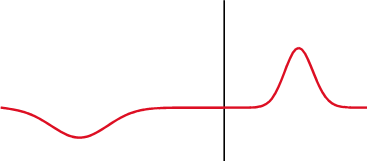
Een signaal wordt gedeeltelijk teruggekaatst daar waar de impedantie verandert.

Fase

Over een weerstand gaan zowel de spanning als de stroom op en neer, ze zouden in fase zijn, maar bij een impedantie is dat anders, de spanning wordt met 1/4 golflengte achter de stroom in een condensator verschoven, en in een inductor naar voren geschoven.

Een 1/4 golflengte wordt meestal weergegeven met het denkbeeldige getal "j", wat ook overeenkomt met een verschuiving van 90 graden.

Het gebruik van het denkbeeldige getal "j" maakt de wiskunde veel eenvoudiger, het laat toe om de totale impedantie op dezelfde manier te berekenen als bij weerstanden, bijvoorbeeld een weerstand plus een impedantie in serie is R+Z, en parallel daaraan is het (R*Z)/(R+Z).

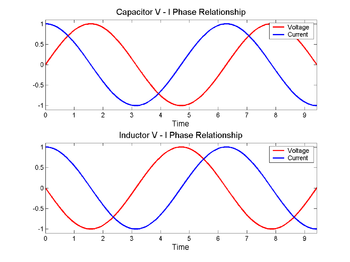
Over een condensator (boven) verandert de spanning (rood) na de stroom (blauw), over een inductor (onder) is het voor. Het faseverschil tussen de spanning en de stroom is 1/4 golflengte.

Vragen en antwoorden

V: Wat is elektrische impedantie?

A: Elektrische impedantie is de hoeveelheid weerstand die een circuit ondervindt bij stroom- of spanningsverandering.

V: Hoe kan elektrische impedantie worden geschreven?

A: Elektrische impedantie kan worden geschreven met de weerstand "R" (reëel deel) en de reactantie "X" (imaginair deel), en met een grootte, fase, grootte en hoek.

V: Wat is het verschil tussen weerstand en impedantie?

A: Het belangrijkste verschil tussen weerstand en impedantie is het woord "verandering"; met andere woorden, de mate van verandering beïnvloedt de impedantie. Weerstand is bestand tegen elke stroom die erdoorheen gaat, terwijl een spoel bestand is tegen veranderingen in de stroom en een condensator bestand is tegen veranderingen in de spanning.

V: Wat zijn enkele formules voor weerstand en impedantie?

A: Voor weerstand, V=R*I waarbij V de spanning is, R de weerstand en I de stroom; voor inductoren Z=j2πfL; voor condensatoren Z=1/j2πfC; waarbij Z staat voor impedantie, j voor imaginair getal -1 , π voor constante pi, f voor frequentie, L voor inductie, C voor capaciteit.

V: Wat zijn enkele natuurkundige verklaringen voor weerstand versus impedantie?

A: Weerstand wordt veroorzaakt door elektronen die met atomen in weerstanden botsen, terwijl de impedantie van een inductor voortkomt uit het creëren van een elektrisch veld en die van een condensator uit het creëren van een magnetisch veld. Bovendien dissiperen weerstanden energie terwijl inductoren en condensatoren energie opslaan die vervolgens kan worden teruggevoerd naar de bron wanneer deze daalt.

V: Hoe berekent u de reflectiecoëfficiënt?

A: De reflectiecoëfficiënt kan worden berekend met Γ=(ZL-ZS)/(ZL+ZS) waarbij Γ (hoofdletter gamma) staat voor reflectiecoëfficiënt; ZS staat voor de impedantie van de bron; ZL staat voor de impedantie van de belasting.