Wat is een frequentieverdeling? Definitie, voorbeelden en uitleg
Leer alles over frequentieverdelingen: duidelijke definitie, praktische voorbeelden en heldere uitleg voor discrete en continue data — begrijp statistiek snel.
In de statistiek is een frequentieverdeling een overzicht van de waarden die een variabele in een steekproef aanneemt, samen met het aantal keren (de frequentie) dat elke waarde voorkomt. Een frequentieverdeling kan discrete waarden direct tellen (bijvoorbeeld antwoorden op een Likert-schaal) of continue waarden groeperen in klassen (bijvoorbeeld lengtes of gewichten). Het doel is om ruwe data compact en inzichtelijk weer te geven, zodat je snel kunt zien welke waarden vaak of juist zelden voorkomen.
Voorbeeld 1 — discrete variabele (Likert-schaal)
Stel dat 100 respondenten een stelling beoordelen op een vijfpunts Likert-schaal (1 = sterk eens, 5 = sterk oneens). Een mogelijke frequentieverdeling van de antwoorden is:
| Antwoord | Frequentie (aantal) | Relatieve frequentie | Cumulatieve frequentie |
|---|---|---|---|
| 1 (sterk eens) | 20 | 20% | 20 |
| 2 | 25 | 25% | 45 |
| 3 | 30 | 30% | 75 |
| 4 | 15 | 15% | 90 |
| 5 (sterk oneens) | 10 | 10% | 100 |
Hieruit zie je direct welke categorieën het meest voorkomen (antwoord 3) en hoe de cumulatieve oplopende telling zich ontwikkelt (handig voor percentielen).
Voorbeeld 2 — continue variabele (lengte van leerlingen)
Voor continue variabelen is het vaak onpraktisch of onmogelijk om elke unieke waarde apart te tellen (er zijn veel verschillende waarden). In dat geval worden waarden gegroepeerd in klassen (intervallen).
| Klasse (cm) | Frequentie | Relatieve frequentie |
|---|---|---|
| 140 – 149 | 3 | 6% |
| 150 – 159 | 12 | 24% |
| 160 – 169 | 20 | 40% |
| 170 – 179 | 10 | 20% |
| 180 – 189 | 5 | 10% |
Bij gegroepeerde frequentietabellen is het gebruikelijk ook de klasse-middenwaarden te berekenen (voor grafische weergave of schatting van het gemiddelde) en eventueel frequentiedichtheid te gebruiken als klassen ongelijk breed zijn.
Belangrijke begrippen
- Frequentie: het aantal waarnemingen in een bepaalde waarde of klasse.
- Relatieve frequentie: de frequentie gedeeld door het totaal (vaak uitgedrukt in procenten). Geeft het aandeel weer.
- Cumulatieve frequentie: de kwartellij van alle frequenties tot en met een bepaalde waarde of klasse. Handig voor percentielen en mediaanbepaling.
- Klassebreedte: het verschil tussen onder- en bovengrens van een klasse bij gegroepeerde data.
- Klasse-midden (midpoint): (ondergrens + bovengrens) / 2, gebruikt bij berekeningen en grafieken.
Hoe maak je een goede frequentieverdeling?
- Bepaal eerst het minimum en maximum van je dataset en het totaal aantal waarnemingen n.
- Kies het aantal klassen (bij grote samples; Sturges' regel: k ≈ 1 + log2(n) is een bruikbare richtlijn, of kies 5–20 klassen afhankelijk van n en doel).
- Bereken de klassebreedte w = (max − min) / k en rond deze zo dat klassen overzichtelijk blijven (bijvoorbeeld op hele getallen).
- Maak aaneengesloten, niet-overlappende klassen die het volledige bereik dekken (bijvoorbeeld 150–159, 160–169, …).
- Tel voor elke (waarde of) klasse het aantal waarnemingen en vul frequentie-, relatieve- en cumulatieve-kolommen in.
- Controleer of de totalen overeenkomen met n en 100% (voor relatieve frequenties).
Grafische weergaves
Veel gebruikte grafieken bij frequentieverdelingen:
- Staafdiagram (bar chart): voor discrete of categorische variabelen (baren met gelijke breedte, zonder aangrenzende balken).
- Histogram: voor gegroepeerde continue variabelen (aangrenzende balken; oppervlak geeft frequentie of frequentiedichtheid).
- Frequentiepolygoon: lijn die klassemidden verbindt; handig om verdelingen te vergelijken.
- Ogive: cumulatieve frequentiegrafiek; handig voor percentielen en mediaan-schatting.
Waarvoor gebruik je een frequentieverdeling?
- Samenvatten van grote datasets zodat patronen zichtbaar worden (modale waarden, spreiding, scheefheid).
- Bepalen van mediaan, modus en percentielen (vaak met behulp van cumulatieve frequenties).
- Basis voor grafieken en verdere statistische analyse (bv. het schatten van het gemiddelde bij gegroepeerde data).
- Identificatie van outliers of onverwachte concentraties van waarden.
Tips en veelgemaakte fouten
- Kies geen te brede klassen: dan verlies je detail. Kies ook geen te smalle klassen: dan wordt de tabel rommelig en minder informatief.
- Voorkom overlappende of gaten tussen klassen (beslis duidelijk of klassen inclusief of exclusief de grenswaarden zijn, bijv. 149,9 of 150).
- Bij ongelijke klassebreedtes werk met frequentiedichtheid (frequentie / breedte) zodat oppervlak van de balken in een histogram correct de frequentie weergeeft.
- Realiseer je dat groeperen informatie vernietigt: resultaten zoals het gemiddelde of variantie berekend uit gegroepeerde data zijn schattingen met een kleine onnauwkeurigheid.
Kort samengevat: een frequentieverdeling zet ruwe data om in een overzichtelijk schema van frequenties (en vaak relatieve en cumulatieve frequenties) en is een basishulpmiddel in de beschrijvende statistiek om patronen en kenmerken van de data snel zichtbaar te maken.

Dit is de bevolkingspiramide van China voor het jaar 2005.
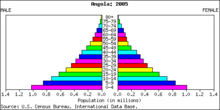
Voorbeeld van een (absolute) frequentieverdeling. Dit is de bevolkingspiramide van Angola, voor het jaar 2005.
Toepassingen
Het beheren en bewerken van gegevens in frequentietabellen is veel eenvoudiger dan het bewerken van ruwe gegevens. Er bestaan eenvoudige algoritmen om uit deze tabellen de mediaan, het gemiddelde (statistiek), de standaardafwijking enz. te berekenen.
Statistische hypothesetests zijn gebaseerd op de beoordeling van verschillen en overeenkomsten tussen frequentieverdelingen. Deze beoordeling omvat maten van centrale tendens of gemiddelden, zoals het gemiddelde en de mediaan, en maten van variabiliteit of statistische spreiding, zoals de standaardafwijking of variantie.
Een frequentieverdeling is scheef wanneer het gemiddelde en de mediaan verschillend zijn. De kurtosis van een frequentieverdeling is de concentratie van scores bij het gemiddelde, of de piek van de verdeling als deze grafisch wordt weergegeven, bijvoorbeeld in een histogram. Als de verdeling meer pieken vertoont dan de normale verdeling, wordt gezegd dat zij leptokurtisch is; als zij minder pieken vertoont, wordt gezegd dat zij platykurtisch is.
Frequentieverdelingen worden ook gebruikt bij frequentieanalyse om codes te kraken en verwijzen naar de relatieve frequentie van letters in verschillende talen.
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Vragen en antwoorden
V: Wat is een frequentieverdeling?
A: Een frequentieverdeling is een lijst van de waarden die een variabele in een steekproef aanneemt, gerangschikt naar hoeveelheid. Het laat zien hoe vaak elke waarde voorkomt.
V: Hoe ziet de frequentieverdeling van antwoorden op een vijfpunts Likert-schaal eruit?
A: De frequentieverdeling van antwoorden op een vijfpunts-Likertschaal zou eruit kunnen zien als een eenvoudige tabel met het aantal mensen dat elk punt op de schaal heeft gewaardeerd.
V: Wat zijn twee nadelen van het gebruik van dit type tabel?
A: Twee nadelen van het gebruik van dit type tabel zijn dat het moeilijk of zelfs onmogelijk kan zijn wanneer het gaat om continue waarden of wanneer er te veel mogelijke waarden zijn.
V: Hoe verschilt dit schema bij het omgaan met continue waarden of grote aantallen mogelijke waarden?
A: Bij continue waarden of grote aantallen mogelijke waarden kan een iets ander schema op basis van het waardenbereik worden gebruikt.
V: Hoe ziet de frequentietabel voor de lengte van de leerlingen eruit?
A: De frequentietabel voor de lengte van leerlingen kan bereiken tonen en hoeveel leerlingen in elk bereik vallen.
V: Welke informatie geeft de frequentieverdeling?
A: De frequentieverdeling geeft informatie over hoe vaak bepaalde variabelen voorkomen in steekproeven en hoe ze verdeeld zijn over die steekproeven.
Zoek in de encyclopedie