Magnetisch moment

Het magnetisch moment van een magneet is een grootheid die bepalend is voor de kracht die de magneet op elektrische stromen kan uitoefenen en voor het koppel dat een magnetisch veld op de magneet zal uitoefenen. Een lus van elektrische stroom, een staafmagneet, een elektron, een molecuul en een planeet hebben allemaal een magnetisch moment.

Zowel het magnetisch moment als het magnetisch veld kunnen worden beschouwd als vectoren met een magnitude en een richting. De richting van het magnetisch moment wijst van de zuid- naar de noordpool van een magneet. Ook het magnetisch veld dat door een magneet wordt geproduceerd, is evenredig met het magnetisch moment. Preciezer gezegd verwijst de term magnetisch moment gewoonlijk naar het magnetisch dipoolmoment van een systeem, dat de eerste term in de multipooluitbreiding van een algemeen magnetisch veld oplevert. De dipoolcomponent van het magnetisch veld van een voorwerp is symmetrisch rond de richting van zijn magnetisch dipoolmoment, en neemt af met de omgekeerde kubus van de afstand tot het voorwerp.

Twee definities van moment

In leerboeken worden twee complementaire benaderingen gebruikt om magnetische momenten te definiëren. In de leerboeken van vóór 1930 werden ze gedefinieerd aan de hand van magnetische polen. In de meeste recente leerboeken worden ze gedefinieerd in termen van Ampèrische stromen.

Definitie van magnetische pool

Natuurkundigen stellen bronnen van magnetische momenten in materialen voor als polen. De noord- en zuidpool zijn een analogie van de positieve en negatieve ladingen in de elektrostatica. Beschouw een staafmagneet met magnetische polen van gelijke magnitude maar tegengestelde polariteit. Elke pool is de bron van een magnetische kracht die zwakker wordt naarmate de afstand toeneemt. Aangezien magnetische polen altijd in paren voorkomen, heffen hun krachten elkaar gedeeltelijk op, want terwijl de ene pool aantrekt, stoot de andere af. Deze opheffing is het grootst wanneer de polen dicht bij elkaar staan, d.w.z. wanneer de staafmagneet kort is. De magnetische kracht van een staafmagneet op een bepaald punt in de ruimte hangt dus af van twee factoren: zowel van de sterkte p {\displaystyle p} $p$ van de polen, als van de vector l {\displaystyle \mathbf {l} $\mathbf {l}$ die ze scheidt. Het moment is gedefinieerd als

m = p l . {\mathbf {m} =p\mathbf {l} . } $\mathbf {m} =p\mathbf {l} .$

Hij wijst in de richting van de zuid- naar de noordpool. De analogie met elektrische dipolen moet niet te ver worden doorgetrokken, want magnetische dipolen zijn geassocieerd met impulsmoment (zie Magnetisch moment en impulsmoment). Niettemin zijn magnetische polen zeer nuttig voor magnetostatische berekeningen, vooral in toepassingen met ferromagneten. Mensen die de magnetische poolbenadering gebruiken, stellen het magnetisch veld over het algemeen voor door het irrotatieveld H {\displaystyle \mathbf {H} } $\mathbf {H}$ , naar analogie van het elektrische veld E {\displaystyle \mathbf {E}} } $\mathbf {E}$ .

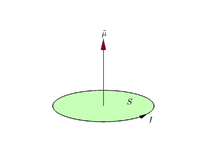
Stroomlus definitie

Stel een vlakke gesloten lus draagt een elektrische stroom I {\displaystyle I} en heeft vectoroppervlak S {\displaystyle \mathbf {S} } $\mathbf {S}$ ( x {\displaystyle x} , y {\displaystyle y} en z {\displaystyle z} $z$ coördinaten van deze vector zijn de gebieden van projecties van de lus op de y z {\displaystyle yz} $yz$ , z x , zx $zx$ en x y {{Displaystyle xy}vlakken). Het magnetisch moment $xy$ m {\displaystyle \mathbf {m} } $\mathbf {m}$ , vector, wordt gedefinieerd als:

m = I S . {\mathbf {m} = I\mathbf {S} . } $\mathbf {m} =I\mathbf {S} .$

Bij conventie wordt de richting van het vectorgebied gegeven door de rechterhandgreepregel (het krullen van de vingers van de rechterhand in de richting van de stroom rond de lus, wanneer de handpalm de buitenrand van de lus "raakt", en de rechte duim de richting van het vectorgebied en dus van het magnetisch moment aangeeft).

Als de lus niet vlak is, wordt het moment gegeven als

m = I 2 ∫ r × d r . {\mathbf {m} ={\frac {I}{2}} keer {\rm {d}} {mathbf {r} . } $\mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} .$

In het meest algemene geval van een willekeurige stroomverdeling in de ruimte kan het magnetisch moment van zo'n verdeling worden gevonden uit de volgende vergelijking:

m = 1 2 ∫ r × J d V , {\mathbf {m} ={\frac {1}{2}} tijden \mathbf {J} V,} $\mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,$

waarbij r {\displaystyle \mathbf {r} } $\mathbf {r}$ de positievector is die vanuit de oorsprong naar de plaats van het volume-element wijst, en J {\displaystyle \mathbf {J} $\mathbf {J}$ is de vector van de stroomdichtheid op die plaats.

De bovengenoemde vergelijking kan voor de berekening van een magnetisch ogenblik van om het even welke assemblage van bewegende lasten, zoals een spinnend geladen vast lichaam worden gebruikt, door te substitueren

J = ρ v , {\mathbf {J} =\rho \mathbf {v} ,} $\mathbf {J} =\rho \mathbf {v} ,$

waarin ρ de elektrische ladingsdichtheid in een bepaald punt $\rho$ is $\mathbf {v}$ en v de momentane lineaire snelheid van dat punt.

Bijvoorbeeld, het magnetisch moment veroorzaakt door een elektrische lading die langs een cirkelvormige baan beweegt is

m = 1 2 q r × v {\displaystyle \mathbf {m} ={\frac {1}{2}},q,\mathbf {r} maal \mathbf {v}} $\mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v}$ ,

waarin r {\displaystyle \mathbf {r} $\mathbf {r}$ de positie van de lading q ten opzichte van het middelpunt van de cirkel is en v de momentane snelheid van de lading is. $\mathbf {v}$

Praktijkmensen die het stroomlusmodel gebruiken, stellen het magnetische veld meestal voor als het solenoïdale veld B {\displaystyle \mathbf {B} } $\mathbf {B}$ analoog aan het elektrostatische veld D {D} } $\mathbf {D}$ .

Magnetisch moment van een solenoïde

Een veralgemening van de bovenstaande stroomlus is een spoel met meerdere windingen, of solenoïde. Het moment is de vectorsom van de momenten van de afzonderlijke windingen. Als de solenoïde N $N$ identieke windingen heeft (enkellaags wikkeling),

m = N I S . {\mathbf {m} =NI\mathbf {S} . } $\mathbf {m} =NI\mathbf {S} .$

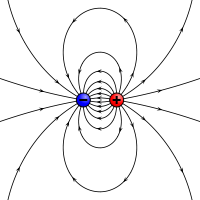
Een elektrostatisch equivalent voor een magnetisch moment: twee tegengestelde ladingen gescheiden door een eindige afstand.

Moment m {\displaystyle \mathbf {m} } $\mathbf {m}$ van een vlakke stroomlus met oppervlakte S {\displaystyle S} $S$ en stroom I {\displaystyle I} .

3-D beeld van een solenoïde.

Eenheden

De eenheid voor het magnetisch moment is geen basiseenheid in het Internationaal Stelsel van Eenheden (SI) en het kan op meer dan één manier worden weergegeven. Bijvoorbeeld, in de definitie van de stroomlus wordt de oppervlakte gemeten in vierkante meter en I {\displaystyle I} wordt gemeten in ampère, zodat het magnetisch moment wordt gemeten in ampère-vierkante meter ( A m 2 {\displaystyle {{A m}}^{2}} ${\text{A m}}^{2}$ ). In de vergelijking voor het koppel op een moment wordt het koppel gemeten in Newton.meters en het magnetisch veld in tesla, dus wordt het moment gemeten in N.m per Tesla ( N.m T - 1 {{N.m T}^{-1}} ${\text{N.m T}}^{-1}$ ). Deze twee voorstellingen zijn gelijkwaardig:

A m 2 = N.m T - 1 . {\an5}^{A m}^{2}= {\an5}^{N.m T}^{-1}. } $\,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}.$

In het CGS-systeem zijn er verschillende reeksen elektromagnetisme-eenheden, waarvan de belangrijkste ESU, Gaussian, en EMU zijn. Daaronder zijn er twee alternatieve (niet-gelijkwaardige) eenheden van magnetisch dipoolmoment in het CGS:

(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (^m2-A of N.m/T)

en (vaker gebruikt)

(EMU CGS en Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (^m2-A of N.m/T).

De verhouding van deze twee niet-equivalente CGS-eenheden (EMU/ESU) is precies gelijk aan de lichtsnelheid in de vrije ruimte, uitgedrukt in cm/s.

Alle formules in dit artikel zijn correct in SI-eenheden, maar in andere eenhedenstelsels moeten de formules wellicht worden gewijzigd. Bijvoorbeeld, in SI-eenheden heeft een stroomlus met stroom I en oppervlakte A het magnetisch moment I×A (zie hieronder), maar in Gaussische eenheden is het magnetisch moment I×A/c.

Intrinsieke magnetische momenten en spins van sommige elementaire deeltjes
Deeltje	Magnetisch dipoolmoment in SI-eenheden (10-27 J/T)	Spin-kwantumgetal (dimensieloos)
elektron	-9284.764	1/2
proton	14.106067	1/2
neutron	-9.66236	1/2
muon	-44.904478	1/2
deuteron	4.3307346	1
triton	15.046094	1/2

Voor het verband tussen de begrippen magnetisch moment en magnetisatie zie magnetisatie.

Vragen en antwoorden

V: Wat is het magnetisch moment van een magneet?

A: Het magnetisch moment van een magneet is een grootheid die de kracht bepaalt die de magneet kan uitoefenen op elektrische stromen en het koppel dat een magnetisch veld erop zal uitoefenen.

V: Welke voorwerpen hebben magnetische momenten?

Antwoord: Een elektrische stroomlus, een staafmagneet, een elektron, een molecuul en een planeet hebben allemaal magnetische momenten.

V: Hoe kunnen zowel het magnetisch moment als het magnetisch veld beschouwd worden?

A: Zowel het magnetisch moment als het magnetisch veld kunnen beschouwd worden als vectoren met een grootte en richting.

V: In welke richting wijst het magnetisch moment in een magneet?

A: De richting van het magnetisch moment wijst van de zuid- naar de noordpool van een magneet.

V: Wat is het verband tussen het magnetisch moment en het magnetisch veld van een magneet?

A: Het magnetisch veld dat door een magneet wordt geproduceerd is evenredig met het magnetisch moment.

V: Waar verwijst de term magnetisch moment normaal naar?

A: Om precies te zijn verwijst de term magnetisch moment normaal naar het magnetische dipoolmoment van een systeem, dat de eerste term in de multipooluitbreiding van een algemeen magnetisch veld produceert.

V: Hoe gedraagt de dipoolcomponent van het magnetische veld van een voorwerp zich als de afstand tot het voorwerp toeneemt?

Antwoord: De dipoolcomponent van het magnetische veld van een voorwerp is symmetrisch rond de richting van zijn magnetisch dipoolmoment, en neemt af als de omgekeerde kubus van de afstand tot het voorwerp.