Oppervlakte-integraal

In de wiskunde is een oppervlakte-integraal een bepaalde integraal over een oppervlak (dat een kromme in de ruimte kan zijn). Net zoals een lijnintegraal één dimensie of één variabele behandelt, kan een oppervlakte-integraal beschouwd worden als een dubbele integraal langs twee dimensies. Gegeven een oppervlak, kan men integreren over zijn scalaire velden (d.w.z. functies die getallen als waarden teruggeven) en vectorvelden (d.w.z. functies die vectoren als waarden teruggeven).

Oppervlakte-integralen hebben toepassingen in de natuurkunde, met name bij de klassieke theorie van het elektromagnetisme.

De definitie van oppervlakte-integraal berust op het opsplitsen van het oppervlak in kleine oppervlakte-elementen.

Een illustratie van een enkel oppervlakte-element. Deze elementen worden infinitesimaal klein gemaakt, door het begrenzingsproces, om het oppervlak te benaderen.

Oppervlakte integralen van scalaire velden

Beschouw een oppervlak S waarop een scalair veld f gedefinieerd is. Als men S beschouwt als gemaakt van een of ander materiaal, en voor elke x in S is het getal f(x) de dichtheid van het materiaal bij x, dan is de oppervlakte-integraal van f over S de massa per dikte-eenheid van S. (Dit is alleen waar als het oppervlak een infinitesimaal dunne schil is.) Een benadering van het berekenen van de oppervlakte-integraal is dan het oppervlak op te delen in vele zeer kleine stukjes, aan te nemen dat op elk stukje de dichtheid ongeveer constant is, de massa per dikte-eenheid van elk stukje te vinden door de dichtheid van het stukje te vermenigvuldigen met de oppervlakte, en dan de resulterende getallen bij elkaar op te tellen om de totale massa per dikte-eenheid van S te vinden.

Om een expliciete formule voor de oppervlakte-integraal te vinden, parametriseren wiskundigen S door op S een stelsel van kromlijnige coördinaten te beschouwen, zoals de lengte- en breedtegraad op een bol. Stel dat zo'n parametrisering x(s, t) is, waarbij (s, t) varieert in een gebied T in het vlak. De oppervlakte-integraal wordt dan gegeven door

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | s d t {{S}f,dS={T}f(\mathbf {x} (s,t))links|{gedeeltelijk \mathbf {x} over een deel van s voor een deel van t} $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

waarbij de uitdrukking tussen de streepjes aan de rechterkant de grootte is van het kruisproduct van de partiële afgeleiden van x(s, t).

Bijvoorbeeld, om de oppervlakte te vinden van een algemene functionele vorm, zeg z = f ( x , y ) {\displaystyle z=f(x,y)} $z=f\,(x,y)$ hebben we

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S},dS=\iint _{T}left {{\partieel \mathbf {r}} over \partieel x} over een deel van y} $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

waarbij r = ( x , y , z ) = ( x , y , f ( x , y ) ) {{r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ . Zodat ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ∂ r ∂ x = 1 , 0 , f x ( x , y ) \over \partieel x}=(1,0,f_{x}(x,y))} ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ , en ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) weergavestijl {{emathbf {r}} over \partieel y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ . Dus,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {Displaystyle {begin{aligned}A&{}==iint _{T}left(1,0,{partiële f over \partiële x}rechts)\left(0,1,{partiële f over \partiële y}rechts)\right(dx,dy)\\\}{}= {sqrt {left({partieel f over \partieel x}}rechts)^{2}+left({partieel f over \partieel y}}rechts)^{2}+1}},x,dy,end{aligned}} ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

dat is de formule die gebruikt wordt voor de oppervlakte van een algemene functionele vorm. Men kan de vector in de tweede regel hierboven herkennen als de normaalvector van het oppervlak.

Merk op dat wegens de aanwezigheid van het kruisproduct, de bovenstaande formules alleen werken voor oppervlakken ingebed in de driedimensionale ruimte.

Oppervlakte integralen van vectorvelden

Beschouw een vectorveld v op S, d.w.z. dat voor elke x in S, v(x) een vector is.

De oppervlakte-integraal kan componentgewijs worden gedefinieerd volgens de definitie van de oppervlakte-integraal van een scalair veld; het resultaat is een vector. Dit geldt bijvoorbeeld voor het elektrisch veld op een vast punt ten gevolge van een elektrisch geladen oppervlak, of de zwaartekracht op een vast punt ten gevolge van een plaat materiaal. Het kan ook de magnetische flux door een oppervlak berekenen.

Als alternatief kunnen wiskundigen de normale component van het vectorveld integreren; het resultaat is een scalair. Een voorbeeld is een vloeistof die door S stroomt, waarbij v(x) de snelheid van de vloeistof op x bepaalt. De flux wordt gedefinieerd als de hoeveelheid vloeistof die in een tijdseenheid door S stroomt.

Deze illustratie impliceert dat als het vectorveld in elk punt raakt aan S, de flux nul is, omdat de vloeistof alleen evenwijdig aan S stroomt, en noch naar binnen noch naar buiten. Dit impliceert ook dat als v niet alleen langs S stroomt, d.w.z. als v zowel een tangentiële als een normale component heeft, alleen de normale component bijdraagt tot de flux. Op basis van deze redenering moeten we, om de flux te vinden, in elk punt het scalair veld nemen van het dotproduct van v met de eenheidsoppervlaknormaal van S, en het verkregen veld integreren zoals hierboven. Dit geeft de formule

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {Displaystyle \int _{S}{\mathbf {v} } }=int _{S}({\mathbf {v} })\,dS=iint _{T}{\mathbf {v} }(\mathbf {x}} (s,t))} }(\mathbf {x} over een deel van s} over een deel van t} rechts)dt,dt. } $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

Het kruisproduct aan de rechterkant van deze uitdrukking is een oppervlaknormaal bepaald door de parametrisering.

Deze formule definieert de integraal aan de linkerkant (let op de punt en de vectornotatie voor het oppervlakte-element).

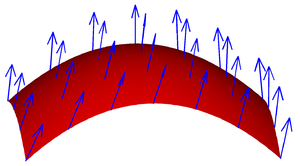
Een vectorveld op een oppervlak.

Stellingen over oppervlakte integralen

Verschillende nuttige resultaten voor oppervlakte-integralen kunnen worden afgeleid met behulp van differentiaalmeetkunde en vectorrekening, zoals de divergentiestelling, en de veralgemening daarvan, de stelling van Stokes.

Gevorderde problemen

Parametrering wijzigen

In de bovenstaande discussie is de oppervlakte-integraal gedefinieerd aan de hand van een parametrisering van het oppervlak S. Een gegeven oppervlak kan verschillende parametriseringen hebben. Wanneer bijvoorbeeld de plaatsen van de noordpool en de zuidpool op een bol worden verplaatst, veranderen de lengte- en breedtegraden voor alle punten op de bol. Een natuurlijke vraag is dan of de definitie van de oppervlakte-integraal afhangt van de gekozen parametrizering. Voor integralen van scalaire velden is het antwoord op deze vraag eenvoudig: de waarde van de oppervlakte-integraal zal dezelfde zijn, ongeacht welke parametrisering men gebruikt.

Integralen van vectorvelden zijn ingewikkelder, omdat de oppervlaktenormaal erbij betrokken is. Wiskundigen hebben bewezen dat gegeven twee parametrizeringen van hetzelfde oppervlak, waarvan de oppervlaktenormalen in dezelfde richting wijzen, beide parametrizeringen dezelfde waarde geven voor de oppervlakte-integraal. Indien echter de normalen van deze parametrizeringen in tegengestelde richtingen wijzen, is de waarde van de oppervlakte-integraal verkregen met de ene parametrizering het negatief van die verkregen met de andere parametrizering. Hieruit volgt dat men, gegeven een oppervlak, geen enkele unieke parametrizering moet aanhouden; maar bij de integratie van vectorvelden moet men wel vooraf beslissen in welke richting de normaal zal wijzen en dan een parametrizering kiezen die met die richting overeenstemt.

Parameterisaties werken op delen van het oppervlak

Een ander probleem is dat oppervlakken soms geen parametrizering hebben die het gehele oppervlak bestrijkt; dit is bijvoorbeeld het geval voor het oppervlak van een cilinder (met eindige hoogte). De voor de hand liggende oplossing is dan om dat oppervlak in verschillende stukken te splitsen, de oppervlakte-integraal op elk stuk te berekenen, en ze dan allemaal op te tellen. Zo werkt het inderdaad, maar bij de integratie van vectorvelden moet men weer voorzichtig zijn met de keuze van de normaalvector voor elk stuk van het oppervlak, zodat wanneer de stukken weer samengevoegd worden, de resultaten consistent zijn. Voor de cilinder betekent dit dat als we besluiten dat voor het zijgebied de normaal uit het lichaam wijst, dan moet voor het bovenste en onderste cirkelvormige deel de normaal ook uit het lichaam wijzen.

Inconsistente oppervlak-normalen

Tenslotte zijn er oppervlakken die niet in elk punt een oppervlaktenormaal hebben met consistente resultaten (b.v. de Möbiusstrook). Als zo'n oppervlak in stukken wordt gesplitst, op elk stuk een parametrisering en overeenkomstige oppervlaktenormaal wordt gekozen, en de stukken weer worden samengevoegd, kunnen de normaalvectoren afkomstig van verschillende stukken niet met elkaar in overeenstemming worden gebracht. Dit betekent dat op een bepaald knooppunt tussen twee stukken de normaalvectoren in tegengestelde richtingen zullen wijzen. Zo'n oppervlak heet niet-oriënteerbaar. Vectorvelden kunnen niet geïntegreerd worden op niet-orienteerbare oppervlakken.

Verwante pagina's

Afwijkingstheorema
Stokes' theorema
Lijnintegraal
Volume-integraal
Cartesiaans coördinatenstelsel
Elementen van volume en oppervlakte in een bolvormig coördinatenstelsel
Elementen van volume en oppervlakte in een cilindrisch coördinatenstelsel
Holstein-Herring methode