De circuitwet van Ampère

Oorspronkelijke circuitwet van Ampère

De wet brengt magnetische velden in verband met elektrische stromen die ze veroorzaken. Een wetenschapper kan de wet van Ampère gebruiken om het magnetische veld te bepalen dat hoort bij een bepaalde stroom of stroom die hoort bij een bepaald magnetisch veld, als er geen in de tijd veranderend elektrisch veld aanwezig is. In zijn oorspronkelijke vorm brengt de Circuitwet van Ampère het magnetisch veld in verband met zijn elektrische stroombron. De wet kan in twee vormen worden geschreven, de "integrale vorm" en de "differentiële vorm". De vormen zijn gelijkwaardig, en aan elkaar gerelateerd door de stelling van Kelvin-Stokes. De wet kan ook worden geschreven in termen van B of H magnetische velden. Ook hier zijn de twee vormen gelijkwaardig (zie het "bewijs" hieronder).

De circuitwet van Ampère is nu bekend als een correcte natuurkundige wet in een magnetostatische situatie: Het systeem is statisch, behalve eventueel voor continue constante stromen binnen gesloten lussen. In alle andere gevallen is de wet onjuist, tenzij de correctie van Maxwell wordt meegenomen (zie hieronder).

Integrale vorm

In SI-eenheden (de versie in cgs-eenheden staat verderop) is de "integrale vorm" van de oorspronkelijke circuitwet van Ampère:

• ∮ C B ⋅ d ℓ = μ 0 ∬ S J ⋅ d S {{C}mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell}} = \mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} }
• ∮ C H ⋅ d ℓ = ∬ S J f ⋅ d S {{C}mathbf {H} \dot \mathrm {d} {{C}mathbf {H}} = \iint _{S}mathbf {J} . . \mathbf {S} }

of gelijkwaardig,

• ∮ C B ⋅ d ℓ = μ 0 I e n c {\displaystyle \mathbf {B} \cdot \mathrm {d} {{c}}==mu _{0}I_{mathrm {enc} }}
• ∮ C H ⋅ d ℓ = I f , e n c {{C}mathbf {H} \I_{mathrm {f,enc}} = I_{mathrm {f,enc} }}

waarbij

• - is het vectordotproduct, ∮ C {{C}} is de gesloten lijnintegraal rond de gesloten kromme C, ∬ S {{S}} is een integraal over het oppervlak S ingesloten door de kromme C (het dubbele integraalteken is alleen bedoeld om aan te geven dat de integraal tweedimensionaal is);
• B is het magnetische B-veld in teslas, H is het magnetische H-veld in ampère per meter;
• I_f,enc is de netto vrije stroom die door het oppervlak S dringt, I_enc is de totale netto stroom die door het oppervlak S dringt, met inbegrip van zowel de vrije als de gebonden stroom.
• J_f is de vrije stroomdichtheid door het oppervlak S ingesloten door de kromme C, J is de totale stroomdichtheid door het oppervlak S ingesloten door de kromme C, met inbegrip van zowel vrije als gebonden stroom;
• dℓ is een infinitesimaal element (een differentiaal) van de kromme C (d.w.z. een vector met grootte gelijk aan de lengte van het infinitesimale lijnelement, en richting gegeven door de raaklijn aan de kromme C), dS is de vectoroppervlakte van een infinitesimaal element van oppervlak S (d.w.z. een vector met grootte gelijk aan de oppervlakte van het infinitesimale oppervlakte-element, en richting normaal aan oppervlak S. De richting van de normaal moet overeenkomen met de oriëntatie van C volgens de rechterhandregel);
• μ₀ is de magnetische constante;

Zie hieronder voor nadere uitleg van de kromme C en het oppervlak S. Er zijn een aantal onduidelijkheden in de bovenstaande definities die om opheldering en een keuze van de conventie vragen.

Ten eerste zijn drie van deze termen gekoppeld aan tekenambiguïteiten: de lijnintegraal ∮ C {{C}} kan in beide richtingen rond de lus gaan (met de klok mee of tegen de klok in); de vectoroppervlakte dS kan in een van de twee richtingen normaal ten opzichte van het oppervlak wijzen; en I_enc is de netto stroom die door het oppervlak S loopt, dat wil zeggen de stroom die in de ene richting loopt, min de stroom in de andere richting - maar beide richtingen kunnen als positief worden gekozen. Deze dubbelzinnigheden worden opgelost door de rechterhandregel: Met de palm van de rechterhand in de richting van het integratiegebied, en de wijsvinger wijzend in de richting van de lijnintegratie, wijst de uitgestrekte duim in de richting die gekozen moet worden voor het vectorgebied dS. Ook de stroom die in dezelfde richting loopt als dS moet als positief worden geteld. De rechterhandgreepregel kan ook worden gebruikt om de tekens te bepalen.

Ten tweede zijn er oneindig veel mogelijke oppervlakken S die de kromme C als grens hebben. (Stel je een zeepfilm voor op een draadlus, die vervormd kan worden door de draad te bewegen). Welk van die oppervlakken moet gekozen worden? Als de lus bijvoorbeeld niet in één vlak ligt, is er geen voor de hand liggende keuze. Het antwoord is dat het niet uitmaakt; bewezen kan worden dat elk oppervlak met grens C kan worden gekozen.

Differentiële vorm

Door de stelling van Kelvin-Stokes kan deze vergelijking ook worden geschreven in een "differentiële vorm". Ook deze vergelijking geldt alleen voor het geval dat het elektrisch veld constant is in de tijd; zie hieronder voor de meer algemene vorm. In SI-eenheden luidt de vergelijking

∇ × B = μ 0 J {\mathbf {J} \mathbf {B} = \mu _{0} \mathbf {J} }

∇ × H = J f {{f}}. \mathbf {H} = \mathbf {J_{f}} }

waarbij

∇ × {{³'displaystyle ³'mathbf {³'nabla } } \ is de kruloperator.  

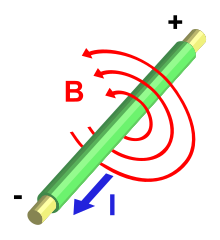
Een elektrische stroom produceert een magnetisch veld.  

Opmerking over vrije stroom versus gebonden stroom

De elektrische stroom die in de eenvoudigste tekstboeksituaties ontstaat, zou als "vrije stroom" worden geclassificeerd. De wet is bijvoorbeeld van toepassing op de stroom die door een draad of batterij loopt. Daarentegen ontstaat "gebonden stroom" in de context van bulkmaterialen die gemagnetiseerd en/of gepolariseerd kunnen worden. (Alle materialen kunnen dat tot op zekere hoogte.)

Wanneer een materiaal wordt gemagnetiseerd (bijvoorbeeld door het in een extern magnetisch veld te plaatsen), blijven de elektronen gebonden aan hun respectieve atomen, maar gedragen zij zich alsof zij in een bepaalde richting om de kern draaien, waardoor een microscopische stroom ontstaat. Wanneer de stromen van al deze atomen worden samengevoegd, creëren zij hetzelfde effect als een macroscopische stroom, die voortdurend rond het gemagnetiseerde voorwerp circuleert. Deze magnetisatiestroom J_M is een bijdrage aan de "gebonden stroom".

De andere bron van gebonden stroom is gebonden lading. Wanneer een elektrisch veld wordt toegepast, kunnen de positieve en negatieve gebonden ladingen zich in polariseerbare materialen over atomaire afstanden van elkaar scheiden, en wanneer de gebonden ladingen bewegen, verandert de polarisatie, waardoor een andere bijdrage aan de "gebonden stroom" ontstaat, de polarisatiestroom J_P .

De totale stroomdichtheid J door vrije en gebonden ladingen is dan:

J = J f + J M + J P , {\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}} \ ,}

met J_f de "vrije" of "geleidende" stroomdichtheid.

Alle stroom is in wezen hetzelfde, microscopisch gezien. Er zijn vaak praktische redenen om gebonden stroom anders te willen behandelen dan vrije stroom. Bijvoorbeeld, de gebonden stroom ontstaat meestal over atomaire dimensies, en men kan willen profiteren van een eenvoudiger theorie die bedoeld is voor grotere dimensies. Het resultaat is dat de meer microscopische wet van Ampère, uitgedrukt in termen van B en de microscopische stroom (die vrije, magnetisatie- en polarisatiestromen omvat), soms in de onderstaande equivalente vorm wordt uitgedrukt in termen van H en de vrije stroom alleen. Voor een gedetailleerde definitie van vrije stroom en gebonden stroom, en het bewijs dat de twee formuleringen gelijkwaardig zijn, zie het onderdeel "bewijs" hieronder.

 

Tekortkomingen van de oorspronkelijke formulering van Ampère's circuitwet

Twee kwesties met betrekking tot de wet van Ampère zijn belangrijk. Ten eerste is er een probleem met de continuïteitsvergelijking voor elektrische lading. Er is een stelling in de vectorrekening die stelt dat de divergentie van een krul altijd nul moet zijn. Dus

∇ ⋅ ( ∇ × B ) = 0 {\displaystyle \nabla çcdot (\mathbf {B}})=0}.

en dus impliceert de oorspronkelijke wet van Ampère dat

∇ J = 0.

Maar in het algemeen

∇ ⋅ J = - ∂ ρ ∂ t {{{{}}}}.

die niet nul is voor een in de tijd variërende ladingsdichtheid. Een voorbeeld hiervan is een condensatorcircuit met in de tijd variërende ladingsdichtheden op de platen.

Ten tweede is er een probleem met de voortplanting van elektromagnetische golven. Bijvoorbeeld, in de vrije ruimte, waar

J = 0.

De wet van Ampère houdt in dat

∇ × B = 0 {\an5}}...

maar in plaats daarvan

∇ × B = - 1 c 2 ∂ E ∂ t {\displaystyle \nabla {B}}=-{frac {1}{c^{2}}}{{frac {mathbf {E}}}{{frac t}}}.

Om deze situaties te behandelen moet de bijdrage van de verplaatsingsstroom worden toegevoegd aan de stroomterm in de wet van Ampère.

James Clerk Maxwell vatte de verplaatsingsstroom op als een polarisatiestroom in de diëlektrische vortexzee, die hij gebruikte om het magnetisch veld te modelleren met water (hydrodynamisch) en met mechanische systemen (mechanisch). Hij voegde deze verplaatsingsstroom toe aan de circuitwet van Ampère bij vergelijking (112) in zijn paper On Physical Lines of Force uit 1861.

Verplaatsingsstroom

In de vrije ruimte is de verplaatsingsstroom gerelateerd aan de tijdsverandering van het elektrische veld.

In een diëlektricum is de bovenstaande bijdrage aan de verplaatsingsstroom ook aanwezig, maar een belangrijke bijdrage aan de verplaatsingsstroom houdt verband met de polarisatie van de afzonderlijke moleculen van het diëlektrische materiaal. Hoewel ladingen in een diëlektricum niet vrij kunnen stromen, kunnen de ladingen in de moleculen zich onder invloed van een elektrisch veld een beetje verplaatsen. De positieve en negatieve ladingen in de moleculen scheiden zich onder het toegepaste veld, waardoor de polarisatietoestand, uitgedrukt als de polarisatiedichtheid P, toeneemt.

Beide bijdragen aan de verplaatsingsstroom worden gecombineerd door de verplaatsingsstroom te definiëren als:

J D = ∂ ∂ t D ( r , t ) , {\displaystyle \mathbf {J_{D}}} ={frac {\partial }{\partial t}} {\mathbf {D} ({\boldsymbol {r}},\t)}.

waarbij het elektrische verplaatsingsveld wordt gedefinieerd als:

D = ε 0 E + P = ε 0 ε r E , {\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +varepsilon {P} =varepsilon _{0}varepsilon _{r}varmathbf {E} \ ,}

waarin ε₀ de elektrische constante is, ε_r de relatieve statische permittiviteit, en P de polarisatiedichtheid. Als we deze vorm voor D in de uitdrukking voor de verplaatsingsstroom substitueren, heeft deze twee componenten:

J D = ε 0 ∂ E ∂ t + ∂ P ∂ t . {\displaystyle \mathbf {J} _{mathrm {D} }=varepsilon _{0}{frac \mathbf {E} }}+{frac {\mathbf {P} } }. }

De eerste term aan de rechterkant is overal aanwezig, zelfs in vacuüm. Er is geen daadwerkelijke verplaatsing van lading mee gemoeid, maar hij heeft wel een bijbehorend magnetisch veld, alsof het een werkelijke stroom is. Sommige auteurs geven alleen aan deze bijdrage de naam verplaatsingsstroom.

De tweede term aan de rechterkant is de verplaatsingsstroom zoals oorspronkelijk bedacht door Maxwell, die samenhangt met de polarisatie van de afzonderlijke moleculen van het diëlektrisch materiaal.

Maxwells oorspronkelijke verklaring voor verplaatsingsstroom richtte zich op de situatie die zich voordoet in diëlektrische media. In het moderne post-aether tijdperk is het concept uitgebreid tot situaties waarin geen materiële media aanwezig zijn, bijvoorbeeld het vacuüm tussen de platen van een opladende vacuümcondensator. De verplaatsingsstroom is vandaag gerechtvaardigd omdat het verscheidene vereisten van een elektromagnetische theorie dient: correcte voorspelling van magnetische velden in gebieden waar geen vrije stroom vloeit; voorspelling van golfpropagatie van elektromagnetische velden; en behoud van elektrische last in gevallen waar de lastendichtheid in de tijd varieert. Voor meer discussie zie Verplaatsingsstroom.

 

Uitbreiding van de oorspronkelijke wet: de Maxwell-Ampère vergelijking

De vergelijking van Ampère werd uitgebreid met de polarisatiestroom, waardoor de beperkte toepasbaarheid van de oorspronkelijke circuitwet van Ampère werd verholpen.

Als vrije ladingen apart van gebonden ladingen worden behandeld, is de vergelijking van Ampère inclusief de correctie van Maxwell in termen van het H-veld (het H-veld wordt gebruikt omdat het de magnetisatiestromen omvat, zodat J_M niet expliciet voorkomt, zie H-veld en ook Noot):

∮ C H ⋅ d ℓ = ∬ S ( J f + ∂ ∂ t D ) ⋅ d A {\displaystyle oint _{C}mathbf {H} \cdot \mathrm {d} = \mathbf {J} \mathrm {f} }+{frac {partieel}{partieel t}}}. \. \mathbf {A} }

(integrale vorm), waarin H het magnetische H-veld is (ook "magnetisch hulpveld", "magnetische veldsterkte", of gewoon "magnetisch veld" genoemd), D het elektrische verplaatsingsveld, en J_f de ingesloten geleidingsstroom of vrije stroomdichtheid. In differentiële vorm,

∇ × H = J f + ∂ ∂ t D . {\mathbf {Nabla} \mathbf {H} = \mathbf {J} _{mathrm {f} }+{{frac {partieel}{{partieel t}}}. \ . }

Als we daarentegen alle ladingen op dezelfde voet behandelen (ongeacht of het gebonden of vrije ladingen zijn), is de veralgemeende vergelijking van Ampère (ook Maxwell-Ampère-vergelijking genoemd) (zie het gedeelte "bewijs" hieronder):

∮ C B ⋅ d ℓ = ∬ S ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) ⋅ d A {\displaystyle oint _{C}mathbf {B} \cdot \mathrm {d} {{C}mathbf {B}}={S}linkse_mathbf {J}  \cdot \mathrm {d} \mathbf {A} }

in integrale vorm. In differentiële vorm,

∇ × B = ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) . {\displaystyle \mathbf {\nabla} \mathbf {B} = (\mathbf {J} + \mu _{0}\epsilon _{0}{frac {{partial t}}}mathbf {E}). )\ . }

In beide vormen omvat J zowel de magnetisatiestroomdichtheid als de geleidings- en polarisatiestroomdichtheid. Dat wil zeggen, de stroomdichtheid aan de rechterkant van de Ampère-Maxwell-vergelijking is:

J f + J D + J M = J f + J P + J M + ε 0 ∂ E ∂ t = J + ε 0 ∂ E ∂ t , {\displaystyle \mathbf {J_{f}+J_{D}+J_{M}} =\mathbf {J_{f}+J_{P}+J_{M}} +varepsilon _{0}{frac {{mathbf {E}} t}}=mathbf {J} +varepsilon _{0}{frac {\mathbf {E} } {\aantal t}}.

waarbij de stroomdichtheid J_D de verplaatsingsstroom is, en J de bijdrage van de stroomdichtheid die feitelijk het gevolg is van de beweging van ladingen, zowel vrije als gebonden. Omdat ∇ - D = ρ, is het ladingcontinuïteitsprobleem met Ampère's oorspronkelijke formulering niet langer een probleem. Door de term in ε₀ ∂E / ∂t is golfvoortplanting in de vrije ruimte nu mogelijk.

Met de toevoeging van de verplaatsingsstroom kon Maxwell (correct) veronderstellen dat licht een vorm van elektromagnetische golf was. Zie elektromagnetische golfvergelijking voor een bespreking van deze belangrijke ontdekking.

Bewijs van gelijkwaardigheid

Bewijs dat de formuleringen van de wet van Ampère in termen van vrije stroom gelijkwaardig zijn aan de formuleringen met betrekking tot totale stroom.

In dit bewijs zullen we aantonen dat de vergelijking ∇ × H = J f + ∂ D ∂ t \nabla \mathbf {H} = \mathbf {J} _{f}+{frac {mathbf {D} t}} is gelijk aan de vergelijking ∇ × B / μ 0 = J + ϵ 0 ∂ E ∂ t {\nabla } \tijden \mathbf {B} /mu _{0}=mathbf {J} + \epsilon _{0}{frac \mathbf {E} }}} Merk op dat we alleen de differentiële vormen behandelen, niet de integrale vormen, maar dat is voldoende omdat de differentiële en integrale vormen in beide gevallen equivalent zijn, volgens de stelling van Kelvin-Stokes. Wij introduceren de polarisatiedichtheid P, die de volgende relatie heeft met E en D: D = ϵ 0 E + P {\mathbf {D} = \epsilon _{0}\mathbf {E} + P } Vervolgens introduceren wij de magnetisatiedichtheid M, die de volgende relatie heeft met B en H: B / μ 0 = H + M {\mathbf {B} /\mu _{0}=\mathbf {H} + M } en het volgende verband met de gebonden stroom: J b o u n d = ∇ × M + ∂ P ∂ t , {{mathbf {J} ¿{mathrm {bound} }= ¿nabla ¿times ¿mathbf {M} +{{frac {mathbf {P}} } {\aantal t}}. = J M + J P , {\an5}... _{mathrm {M} }+\mathbf {J} _{mathrm {P} }\ ,} waarbij J M = ∇ × M , {{emathbf {J} _{mathrm {M} }= \nabla \mathbf {M} \ ,} wordt de magnetisatiestroomdichtheid genoemd, en J P = ∂ P ∂ t , {\displaystyle J} _{mathrm {P} }={frac \mathbf {P} }{{mathrm {P}}}. is de polarisatiestroomdichtheid. Als we de vergelijking voor B: ∇ × B / μ 0 = ∇ × ( H + M ) {\displaystyle \mathbf {\nabla} \mathbf {B} /mu _{0}= \mathbf {nabla } \tijden \links(\mathbf {H+M} \rechts)}. = ∇ × H + J M {\mathbf {H} \mathbf {H} + J_{M}} } = J f + J P + ε 0 ∂ E ∂ t + J M {\displaystyle =J_{f}} + J_{P}} +varepsilon _{0}{frac \mathbf {E} }} +varepsilon _{0}{frac \mathbf {E}}}. } Bijgevolg, verwijzend naar de definitie van de gebonden stroom: ∇ × B / μ 0 = J f + J b o u n d + ε 0 ∂ E ∂ t {\displaystyle \nabla } \mathbf {B} /\mu _{0}=\mathbf {J_{f}} +{0}==mathbf {J_{f}} _{mathrm {bound} }+\varepsilon _{0}{frac {{mathbf {E} }}} = J + ε 0 ∂ E ∂ t , {\displaystyle =mathbf {J} +varepsilon _{0}{frac {mathbf {E} }{{{} t}}. zoals te zien was.

 

Wet van Ampère in cgs eenheden

In cgs-eenheden luidt de integraalvorm van de vergelijking, met inbegrip van de correctie van Maxwell, als volgt

∮ C B ⋅ d ℓ = 1 c ∬ S ( 4 π J + ∂ E ∂ t ) ⋅ d S {\displaystyle oint _{C}mathbf {B} \dot \mathrm {d} {\boldsymbool {\ell}}={{frac {1}{c}}{iint _{S}}{{left}(4pi \mathbf {J} +{{{frac {\partial \mathbf {E}}{{{{partial t}}}}{cdot \mathrm {d} \mathbf {S} }

waarbij c de lichtsnelheid is.

De differentiële vorm van de vergelijking (nogmaals, met inbegrip van de correctie van Maxwell) is

∇ × B = 1 c ( 4 π J + ∂ E ∂ t ) . {\displaystyle \mathbf {\nabla} \times \mathbf {B} ={{frac {1}{c}}{left (4 \pi \mathbf {J} +{{frac {\mathbf {E} }{{\partial t}}). }  

Verwante pagina's