Trigonometrische functie

In de wiskunde zijn de goniometrische functies een reeks functies die hoeken relateren aan de zijden van een rechthoekige driehoek. Er zijn vele goniometrische functies, waarvan de drie meest voorkomende sinus, cosinus en tangens zijn, gevolgd door cotangens, secans en cosecans. De laatste drie worden reciproke goniometrische functies genoemd, omdat ze werken als de reciproke van andere functies. Secans en cosecans worden zelden gebruikt.

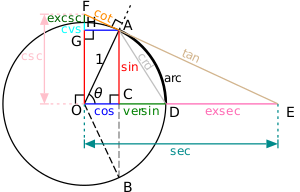
  Alle goniometrische functies van alle hoeken kunnen worden geconstrueerd met behulp van een cirkel met middelpunt O en straal 1.  Zoom
Alle goniometrische functies van alle hoeken kunnen worden geconstrueerd met behulp van een cirkel met middelpunt O en straal 1.  

Trigonometrische functies: Sinus , cosinus , tangens , cosecans , secans en cotangens.  Zoom
Trigonometrische functies: Sinus , cosinus , tangens , cosecans , secans en cotangens.  

Definitie

De goniometrische functies worden soms ook cirkelfuncties genoemd. Het zijn functies van een hoek; ze zijn belangrijk bij de studie van driehoeken, naast vele andere toepassingen. Trigonometrische functies worden gewoonlijk gedefinieerd als verhoudingen van twee zijden van een rechthoekige driehoek die de hoek bevat, en kunnen ook worden gedefinieerd als de lengten van verschillende lijnstukken van een eenheidscirkel (een cirkel met een straal van één).

Definities van rechthoekige driehoeken

Om de goniometrische functies voor de hoek A te definiëren, begin je met een rechthoekige driehoek die de hoek A bevat:

We gebruiken de volgende namen voor de zijden van de driehoek:

  • De hypotenusa is de zijde tegenover de rechte hoek, of gedefinieerd als de langste zijde van een rechthoekige driehoek, in dit geval h.
  • De overstaande zijde is de zijde tegenover de hoek waarin we geïnteresseerd zijn, in dit geval a.
  • De aanliggende zijde is de zijde die in contact staat met de hoek waarin we geïnteresseerd zijn en de rechte hoek, vandaar de naam. In dit geval is de aanliggende zijde b.

Alle driehoeken bestaan in de Euclidische meetkunde zo dat de som van de binnenhoeken van elke driehoek π radialen (of 180°) bedraagt; voor een rechthoekige driehoek liggen de twee niet-rechtse hoeken dus tussen nul en π/2 radialen. De lezer dient op te merken dat de volgende definities strikt genomen alleen de goniometrische functies voor hoeken in dit bereik definiëren. Wij breiden ze uit tot de volledige reeks reële argumenten door de eenheidscirkel te gebruiken, of door bepaalde symmetrieën en periodieke functies te eisen.

1) De sinus van een hoek is de verhouding tussen de lengte van de overstaande zijde en de lengte van de schuine zijde. In ons geval

sin A = tegenovergestelde hypotenusa = a h . {sin A = tegenovergestelde hypotenusa = a h . } {\displaystyle \sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {a}{h}}.}

Merk op dat deze verhouding niet afhangt van de gekozen rechthoekige driehoek, zolang deze de hoek A bevat, aangezien al deze driehoeken gelijk zijn.

De verzameling nulpunten van sinus (d.w.z. de waarden van xx waarvoor sin x = 0 {displaystyle \sin x=0}{\displaystyle \sin x=0} ) is

{n π | n ∈ Z } . {\a6}{\a6}in \mathbb {Z}. \rechts.} } {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}.}

2) De cosinus van een hoek is de verhouding van de lengte van de aanliggende zijde tot de lengte van de schuine zijde. In ons geval

cos A = aangrenzende hypotenusa = b h . {\displaystyle \cos A={{{\textrm {adjacent}}{{\textrm {hypotenuse}}}={{\frac {b}{h}}. } {\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{h}}.}

De verzameling nulpunten van de cosinus is

{ π 2 + n π | n ∈ Z } . {{frac {\pi }{2}}+n\pi {\bigg |}}n\in \mathbb {Z}}. \.} } {\displaystyle \left\{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \right\}.}

3) De tangens van een hoek is de verhouding van de lengte van de overstaande zijde tot de lengte van de aanliggende zijde. In ons geval

tan A = tegenover aangrenzend = a b . {\displaystyle \tan A={{frac {textrm {opposite}}{{textrm {adjacent}}}={{frac {a}{b}}. } {\displaystyle \tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}.}

De verzameling nulpunten van de tangens is

{n π | n ∈ Z } . {\a6}{\a6}in \mathbb {Z}. \rechts.} } {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}.}

Dezelfde reeks van de sinusfunctie sinds

tan A = sin A cos A . {\displaystyle \tan A={frac {sin A}{cos A}}. } {\displaystyle \tan A={\frac {\sin A}{\cos A}}.}

De overige drie functies kunnen het best worden gedefinieerd aan de hand van bovenstaande drie functies.

4) De cosecans csc(A) is het multiplicatieve inverse van sin(A), d.w.z. de verhouding van de lengte van de schuine zijde tot de lengte van de overstaande zijde:

csc A = hypotenusa tegenover = h a {csc A={{frac {hypotenusa}}{{textrm {opposite}}}={{frac {h}{a}}}{\displaystyle \csc A={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}} .

5) De secans sec(A) is het multiplicatieve inverse van cos(A), d.w.z. de verhouding van de lengte van de schuine zijde tot de lengte van de aangrenzende zijde:

sec A = hypotenusa aangrenzend = h b {sec A={{frac {hypotenusa}}{{textrm {aangrenzend}}}={{frac {h}{b}}}{\displaystyle \sec A={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {h}{b}}} .

6) De cotangens cot(A) is het multiplicatieve inverse van tan(A), d.w.z. de verhouding van de lengte van de aanliggende zijde tot de lengte van de tegenoverliggende zijde:

cot A = aangrenzend tegenover = b a {{{{}}}={{{{{{}extrm {a}}}}{\displaystyle \cot A={\frac {\textrm {adjacent}}{\textrm {opposite}}}={\frac {b}{a}}} .

Definities door machtsreeksen

Men kan de goniometrische functies ook definiëren met behulp van machtsreeksen:

sin x = x - x 3 3 ! + x 5 5 ! - x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{{{frac {x^{3}}{3!}}+{{frac {x^{5}}{5!}}-{{{frac {x^{7}}{7!}}+{cdots =\sum _{n=0}^{{{{frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}. {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}

cos x = 1 - x 2 2 ! + x 4 4 ! - x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{{frac {x^{2}}{2!}}+{{frac {x^{4}}{4!}}-{{frac {x^{6}}{6!}}+{cdots =\sum _{n=0}^{{infty }{{{frac {(-1)^{n}x^{2n}}{(2n)!}}. {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}

en definieer tangens, cotangens, secans en cosecans met behulp van identiteiten, zie hieronder.

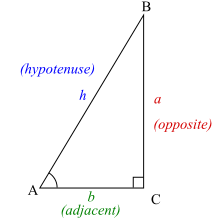
 Een rechthoekige driehoek bevat altijd een hoek van 90° (π/2 radialen), hier aangeduid met C. Hoeken A en B kunnen variëren. Trigonometrische functies geven het verband aan tussen de lengte van de zijden en de binnenhoeken van een rechthoekige driehoek.Zoom
Een rechthoekige driehoek bevat altijd een hoek van 90° (π/2 radialen), hier aangeduid met C. Hoeken A en B kunnen variëren. Trigonometrische functies geven het verband aan tussen de lengte van de zijden en de binnenhoeken van een rechthoekige driehoek.

Identiteiten

Enkele belangrijke identiteiten:

tan x = sin x cos x {{frac {sin x}{cos x}}}. {\displaystyle \tan x={\frac {\sin x}{\cos x}}}

cot x = cos x sin x {{{frac {cos x}{sin x}}}. {\displaystyle \cot x={\frac {\cos x}{\sin x}}}

sec x = 1 cos x {sec x={{frac {1}{cos x}}}. {\displaystyle \sec x={\frac {1}{\cos x}}}

csc x = 1 sin x {{cscsc x={frac {1}{sin x}}}. {\displaystyle \csc x={\frac {1}{\sin x}}}

sin 2 x + cos 2 x = 1 {displaystyle ^{2}x+\cos ^{2}x=1} {\displaystyle \sin ^{2}x+\cos ^{2}x=1}

sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin xcos x} {\displaystyle \sin 2x=2\sin x\cos x}

cos 2 x = cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x-\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x} {\displaystyle \cos 2x=\cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}

tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={frac {2\tan x}{1-\tan ^{2}x}}. {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}

sin ( x ± y ) = sin x cos y ± cos x sin y {displaystyle \sin \left(xpm y) = \sin xcos ypm \sin y}. {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}

cos ( x ± y ) = cos x cos y ∓ sin x sin y {\displaystyle \cos \left(xpm y) = \cos x ymp \in xsin y} {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}

tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(xpm y) ={frac {\tan xpm \tan y}{1mp \tan x\tan y}}}. {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}}  

Hyperbolische functies

De hyperbolische functies zijn als de goniometrische functies in die zin dat zij zeer vergelijkbare eigenschappen hebben. Ze worden gedefinieerd in termen van de exponentiële functie, die gebaseerd is op de constante e.

  • Hyperbolische sinus:

sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={{frac {e^{x}-e^{-x}{2}}={frac {e^{2x}-1}{2e^{x}}={{frac {1-e^{-2x}}{2e^{-x}}. } {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}.}

  • Hyperbolische cosinus:

cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={frac {e^{x}+e^{-x}{2}}={frac {e^{2x}+1}{2e^{x}}={{frac {1+e^{-2x}}{2e^{-x}}}. } {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.}

  • Hyperbolische tangens:

tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={frac {sinh x}{cosh x}}={frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={frac {e^{2x}-1}{e^{2x}+1}}={{frac {1-e^{-2x}}{1+e^{-2x}}}. } {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}={\frac {1-e^{-2x}}{1+e^{-2x}}}.}

  • Hyperbolische cotangens:

coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={frac {cosh x}{sinh x}}={{frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={{frac {e^{2x}+1}{e^{2x}-1}}={{{frac {1+e^{-2x}}{1-e^{-2x}}}},\qquad x{neq 0.}. {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}},\qquad x\neq 0.}

  • Hyperbolische secans:

sech x = 1 cosh x = 2 e x + e - x = 2 e x e 2 x + 1 = 2 e - x 1 + e - 2 x . {\displaystyle \operatorname {sech} \x={frac {1}{cosh x}}={frac {2}{e^{x}+e^{-x}}}={frac {2e^{x}}{e^{2x}+1}}={frac {2e^{-x}}{1+e^{-2x}}}. } {\displaystyle \operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}.}

  • Hyperbolische cosecans:

csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \x={{frac {1}{sinh x}}={{frac {2}{e^{x}-e^{-x}}}={frac {2e^{x}}{e^{2x}-1}}={frac {2e^{-x}}{1-e^{-2x}}},\kwadraat xneq 0.} {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}},\qquad x\neq 0.}  

Gerelateerde pagina's

 

AlegsaOnline.com - 2020 / 2023 - License CC3