Wereldlijn | het unieke pad dat een object heeft als het door zowel ruimte als tijd reist
Een wereldlijn is het unieke pad dat een voorwerp heeft als het door zowel ruimte als tijd reist, meestal ruimtetijd genoemd. Zoals we leren van de speciale relativiteit, geldt dat hoe sneller een voorwerp gaat, hoe meer de tijd vertraagt voor dat voorwerp. Zoals u in de afbeelding hiernaast kunt zien, verloopt de tijd voor het langzamere object sneller dan voor het zeer snelle object, waarvoor de tijd veel langzamer verloopt. Wanneer een voorwerp de lichtsnelheid bereikt, zal het nul zijn op de t-as, wat betekent dat het geen vooruitgang heeft geboekt in de tijdsrichting. In principe tonen de wereldlijnen aan dat wanneer de lichtsnelheid wordt bereikt, de tijd voor de waarnemer stopt. Wereldlijnen worden zeer vaak gebruikt in de theoretische natuurkunde en de speciale relativiteit, evenals in de algemene relativiteit.
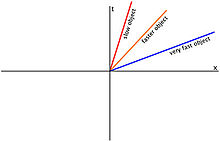
De verschillende paden van drie voorwerpen die met verschillende snelheden gaan en hun respectieve metingen van het verstrijken van de tijd, waarbij de t-as het verstrijken van de tijd voorstelt en de x-as de snelheid van het voorwerp.
Gebruik
Het concept van wereldlijnen wordt veel gebruikt in de theoretische natuurkunde, omdat het een aantal interessante feiten laat zien over beweging met hoge snelheid. Zo is de tijddilatatievergelijking van Albert Einstein algebraïsch ongedefinieerd wanneer de snelheid van een voorwerp de lichtsnelheid is, maar met behulp van wereldlijnen kan men vaststellen dat wanneer de snelheid de lichtsnelheid is, de tijd stopt. Hoewel Einsteins vergelijking (voor tijddilatatie) aantoont dat een voorwerp dat sneller gaat dan het licht, teruggaat in de tijd, kan hetzelfde concept worden beschreven met behulp van wereldlijnen.
| Deel van een reeks artikelen over | ||||||
| Algemene relativiteit | ||||||
|
| ||||||
| ·
·
| ||||||
| Fundamentele concepten
| ||||||
| Fenomenen
| ||||||
| ||||||
| Oplossingen
| ||||||
Vragen en antwoorden
V: Wat is een wereldlijn?
A: Een wereldlijn is het unieke pad dat een voorwerp heeft als het door ruimte en tijd reist, meestal ruimtetijd genoemd.
V: Hoe verklaart de speciale relativiteit hoe de tijd verstrijkt voor voorwerpen die met verschillende snelheden reizen?
A: Volgens de speciale relativiteit gaat de tijd voor een object langzamer naarmate het sneller gaat. Het langzamere voorwerp gaat sneller dan het zeer snelle voorwerp, wat betekent dat de tijd voor hen veel langzamer verstrijkt.
V: Wat gebeurt er wanneer een voorwerp de lichtsnelheid bereikt?
Antwoord: Wanneer een voorwerp de lichtsnelheid bereikt, zal het nul zijn op de t-as, wat betekent dat het geen vooruitgang heeft geboekt in de tijdsrichting. Dit betekent dat de tijd voor de waarnemer stopt.
V: Op welke gebieden worden wereldlijnen gebruikt?
A: Wereldlijnen worden zeer vaak gebruikt in de theoretische natuurkunde en de speciale relativiteit, alsmede in de algemene relativiteit.
V: Hoe kunnen wij een wereldlijn visualiseren?
A: Wij kunnen een wereldlijn visualiseren door naar illustraties te kijken die laten zien hoe objecten die met verschillende snelheden reizen verschillende snelheden van verstrijken ervaren.
V: Is er een manier om een eenmaal vastgestelde wereldlijn te veranderen?
Antwoord: Als een wereldlijn eenmaal is vastgesteld, kan hij niet meer worden veranderd, omdat hij een onveranderlijk pad door de ruimtetijd vertegenwoordigt.
V: Waar verwijst de "t-as" naar met betrekking tot het bereiken van de lichtsnelheid? A: De "t-as" verwijst naar vooruitgang in termen van tijd - wanneer een voorwerp de lichtsnelheid bereikt, is zijn vooruitgang in termen van tijd nul op deze as, wat betekent dat er geen vooruitgang is geboekt in termen van het passeren van de ruimtetijd.
Zoek in de encyclopedie

