De wetten van Kepler
De wetten van Kepler over de beweging van planeten zijn drie wetten die de beweging van planeten rond de zon beschrijven:
- Planeten bewegen rond de zon in elliptische banen. De zon bevindt zich in een van de twee brandpunten van de baan.
- Een lijnstuk dat een planeet en de zon met elkaar verbindt, neemt gelijke gebieden in gelijke tijdsintervallen in beslag.
- Het kwadraat van de omlooptijd van een planeet is evenredig met de kubus van de halve lange as van zijn baan.
Johannes Kepler vond deze wetten, tussen 1609 en 1619.
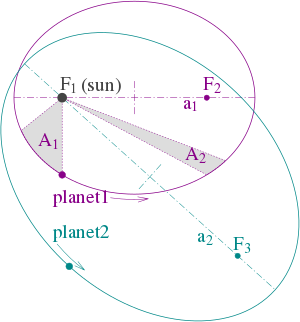
Figuur 1: Illustratie van de drie wetten van Kepler met twee planeetbanen. (1) De banen zijn ellipsen, met brandpunten ƒ1 en ƒ2 voor de eerste planeet en ƒ1 en ƒ3 voor de tweede planeet. De zon staat in brandpunt ƒ1 . (2) De twee gearceerde sectoren A1 en A2 hebben dezelfde oppervlakte en de tijd voor planeet 1 om segment A1 af te leggen is gelijk aan de tijd om segment A2 af te leggen. (3) De totale omlooptijden voor planeet 1 en planeet 2 hebben een verhouding a13/2 : a23/2 .
Vergelijking met Copernicus
De wetten van Kepler verbeteren het model van Copernicus. Als de excentriciteiten van de planeetbanen op nul worden gesteld, is Kepler het in principe eens met Copernicus:
- De planeetbaan is een cirkel
- De zon in het centrum van de baan
- De snelheid van de planeet in de baan is constant
De excentriciteiten van de banen van de planeten die Copernicus en Kepler kenden zijn klein, dus de bovenstaande regels geven goede benaderingen van de planeetbeweging; maar de wetten van Kepler passen beter bij de waarnemingen dan die van Copernicus.
De correcties van Kepler liggen helemaal niet voor de hand:
- De planeetbaan is geen cirkel, maar een ellips.
- De zon staat niet in het centrum maar in een brandpunt van de elliptische baan.
- Noch de lineaire snelheid noch de hoeksnelheid van de planeet in de baan is constant, maar de oppervlaktesnelheid is constant.
De excentriciteit van de aardbaan maakt de tijd van de maartnachtevening tot de septembernachtevening, ongeveer 186 dagen, ongelijk aan de tijd van de septembernachtevening tot de maartnachtevening, ongeveer 179 dagen. Een diameter zou de baan in gelijke delen snijden, maar het vlak door de zon evenwijdig aan de evenaar van de aarde snijdt de baan in twee delen met oppervlakten in een verhouding van 186 tot 179, dus de excentriciteit van de aardbaan bedraagt ongeveer
ε ≈ π 4 186 - 179 186 + 179 ≈ 0,015 , {varepsilon \frac {{4}}}{frac {186-179}{186+179}} } }approx 0,015,}.
wat dicht bij de juiste waarde ligt (0,016710219) (zie de aardbaan). De berekening is correct wanneer het perihelium, de datum waarop de aarde het dichtst bij de zon staat, op een zonnewende valt. Het huidige perihelium, nabij 4 januari, ligt vrij dicht bij de zonnewende van 21 december.
Zoek in de encyclopedie
