Lineaire functie

In de basiswiskunde is een lineaire functie een functie waarvan de grafiek een rechte lijn is in 2-dimensies (zie afbeeldingen). Een voorbeeld is: y=2x-1. In de hogere wiskunde verwijst een lineaire functie vaak naar een lineaire afbeelding.

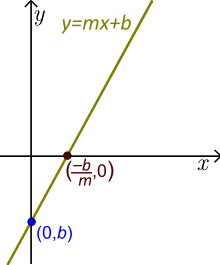
Lineaire functie (De lijn hier is generiek. Hij is schuin dus m≠0. Zie voorbeelden met werkelijke waarden voor m en b hieronder.)

Basiseigenschappen

Formeel is een lineaire functie een functie f(x):R→R zodanig dat de grafiek van f een rechte is. Dit betekent dat het domein of de invoer van f een reëel getal R is en dat het bereik of de uitvoer van f ook een reëel getal R is. Meestal schrijven we y(x) of gewoon y in plaats van f(x). De formele verklaring betekent dus:

voeren we een reëel getal x in of voegen we dat toe aan de lineaire functie
de lineaire functie levert of geeft een reëel getal y en
al deze punten (x,y) vormen een lijn.

Er zijn drie hoofdvormen om lineaire functies te schrijven: hellingshoek-intercept, standaard en parametrisch.

Schuine streep vorm

De helling-interceptvorm (ook wel punt-hoek of expliciet genoemd) van een lineaire functie is y ( x ) = m x + b {\displaystyle y(x)=mx+b} $y(x)=mx+b$ of y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Deze vorm heeft 2 variabelen x en у en 2 constanten m en b.

De letters m en b zijn constanten. Voordat we met een lineaire functie werken, vervangen we m en b door reële getallen.
De letters x en y zijn variabelen.

De variabele x wordt de onafhankelijke variabele of het argument genoemd. Elk reëel getal x kan worden ingevoerd of gesubstitueerd in een lineaire functie. De functie geeft dan de overeenkomstige waarde voor y.
De variabele y wordt de afhankelijke variabele genoemd. Het is de outputwaarde na vervanging van een inputwaarde voor x.

Horizontale lijnen zijn inbegrepen. De lijn is horizontaal als en slechts als m=0. Dan hebben we gewoon y=b. Aangezien b een reëel getal is, is dit een constante functie. Dus een constante functie is ook een lineaire functie.
Verticale lijnen worden nooit opgenomen omdat een verticale lijn geen functie is. Een verticale lijn doorstaat de verticale lijntest niet. (Een verticale lijn wordt gedefinieerd door de vergelijking: x=b waarbij b een reëel getal is).
Schuine lijnen zijn inbegrepen. De lijn is schuin als en slechts als m≠0.

De hellingshoekvorm is uniek. Een andere waarde van m of een andere waarde van b geeft een andere lijn.
Een lineaire functie is een polynoomfunctie van de eerste of nulgraad in één variabele х .
De constante term is b. Als we x=0 in de functie substitueren, krijgen we y=b. Het getal b is dus het y-intercept en de lijn kruist de у-as in het punt (0,b).
Als m≠0, is het getal^–b /_m het x-intercept of de wortel of nul en (^–b /_m ,0) het punt waar de lijn de х-as snijdt. Hier is de waarde van de functie nul.
De coëfficiënt m van x wordt de helling of het hellingspercentage van de lijn genoemd. Voor elke lijn is het getal m een constante en dus is de helling constant voor de hele lijn. De helling bepaalt zowel de richting als de steilheid van de lijn. Richting en steilheid worden de veranderingssnelheid genoemd. De veranderingssnelheid is dus m en is constant voor elke lijn.

Het teken van m bepaalt de richting. Als m>0 dan is de lineaire functie stijgend; als m<0 dan is de functie dalend.
De absolute waarde van m bepaalt de steilheid. Als |m|<1 dan is de helling zacht; als |m|>1 dan is de helling steil.
Als de helling van een rechte m is en (х,у) een willekeurig punt op de rechte is, moet ook het punt (х+1, y+m) op de rechte liggen.

Voorbeeld: y=-2x+4. De helling is m= -2 en het y-intercept is b=4 of het punt (0,4). Door y=0 in te vullen en op te lossen voor x, krijgen we 0=-2x+4 of x=2. Dus x=2 is de wortel van deze lineaire functie en het punt (2,0) is het x-intercept. Aangezien de helling m = -2 is, is de lijn dalend. Aangezien |-2|=2>1, is de daling relatief sterk. Voor elke verandering in х van 1 (naar rechts), verandert de waarde van у -2 (gaat naar beneden).

De grafiek van een lijn wordt bepaald door twee punten. Om een lineaire functie te tekenen, kunnen we twee verschillende waarden voor x in de functie invullen en de bijbehorende y-waarden oplossen. We tekenen deze twee punten. Met een liniaal trekken we de lijn door deze twee punten en trekken hem langs beide punten.

Voorbeeld: y=-2x+4. Door x=0 in te vullen krijgen we y=4 (dit is het y-intercept) en dus het punt (0,4). Als we x=1 vervangen, krijgen we y=2 en dus het punt (1,2). Plot deze punten en trek de lijn. (Merk op dat het 2e punt 1 naar rechts en 2 naar beneden ligt van het 1e punt. Zoals we in het bovenstaande voorbeeld zeiden, gebeurt dit omdat de helling m= -2 is)

Een lineaire functie die geen constante functie is, is een bijectie. Zij geeft elk reëel getal weer (surjectie) voor precies één invoerwaarde (injectie).

Voorbeeld: y= -x+2. Stel dat y= -1. We substitueren y= -1 en krijgen: -1= -'x+2 of x=3. Dit is de enige oplossing. We kunnen dit doen voor elke y-waarde.

Standaardformulier

A x + B y = C , B ≠ 0 {Displaystyle Ax+By=C,\,Bneq 0} $Ax+By=C,\,B\neq 0$ .

De standaardvorm heeft 2 variabelen x en у en 3 constanten A, B en C die voor het werken worden vervangen door reële getallen. Deze vorm wordt vaak gebruikt in de meetkunde en in stelsels van lineaire vergelijkingen.

Voorbeeld: De lineaire functie 3x-2y=1 staat in standaardvorm. De constanten zijn A=3, B=-2 en C=1.

Deze vorm wordt soms geschreven als: A x + B y + C = 0 {Displaystyle Ax+By+C=0} $Ax+By+C=0$ . Dus in plaats van 3x-2y=1 schrijven we de equivalente vergelijking 3x-2y-1=0.
De constanten A, B en C zijn niet uniek bepaald. Als we ze met een factor k vermenigvuldigen, verandert de waarde van deze constanten, maar de lijn blijft dezelfde.

Voorbeeld: De lijnen 3x-2y=1 en 6x-4y=2 vallen samen (dezelfde lijn). Hier is de factor: k=2. We vermenigvuldigen de eerste vergelijking met 2 om de tweede vergelijking te krijgen. De unieke hellingshoekvorm van deze rechte is: y=1,5x-0,5 (los beide vergelijkingen op voor y).

Vector-Parametrische vorm

Parametrische vorm: { x ( t ) = x 1 + a 1 t y ( t ) = y 1 + a 2 t a 1 ≠ 0 , t ∈ R {displaystyle \left}{{begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}{y(t)={y_{1}+{a_{2}}t}}end{array}}}.\. $\left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ of...

Vectorvorm: X = ( x 1 , y 1 ) + t ( a 1 , a 2 ) {\displaystyle {\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})} ${\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})$ of r ( t ) = < x 1 + a 1 t , y 1 + a 2 t > , a 1 ≠ 0 , t ∈ R {displaystyle r(t)=,<x_{1}+a_{1}t,¿,y_{1}+a_{2}t>,,¿,{a_{1}neq 0},,¿,t in \mathbb {R} }. $r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,,\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ .

De parametrische of vector-parametrische vorm heeft 1 parameter t, 2 variabelen x en у, en 4 constanten a₁ , a₂ , x₁ , en y₁ . De coëfficiënten a₁ , a₂ , x₁ , en y₁ zijn niet uniek bepaald. De lijn gaat door de punten А=(x₁ , y₁ ) en B=(x₁ +a₁ , y₁ +a₂ ) zodat het nemen van andere punten of zelfs maar het omkeren van de volgorde van de punten zal leiden tot andere constanten voor dezelfde lijn.
De parameter t is niet zichtbaar in de grafiek.
Ingenieurs gebruiken meestal de letter t voor de parameter. Wiskundigen gebruiken vaak de Griekse letter λ.

Voorbeeld: X=(-1,1)+t(2,3), t∈R is een lijn in vectorvorm. Hierbij geldt: a₁ =2, a₂ =3, x₁ =-1 en x₂ =1. De rechte gaat door de punten (x₁ ,y₁ )=(-1,1) en (x₁ +a₁ ,y₁ +a₂ )=(1,4). De overeenkomstige parametrische vorm van deze rechte is: x(t)= -1+2t, y(t)=1+3t. De unieke hellingshoekvorm van deze rechte is: y(x)=1,5x+2,5 (los de eerste vergelijking op voor t en substitueer dit resultaat in de tweede vergelijking).

De vector-parametrische vorm van een lijn strekt zich op natuurlijke wijze uit tot lijnen in 3-dimensionale en hogere ruimten. De andere vormen niet.

Voorbeeld: X=(-1,1,2)+t(2,3,-1), t∈R is een lijn in de 3-dimensionale ruimte. De rechte gaat door de punten (-1,1,2) en (1,4,1).

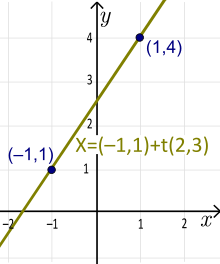
Vector-parametrische vorm van een lijn (niet-uniek). De unieke hellingshoekvorm is y=1,5x+2,5

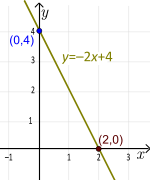
Helling-intercept vorm van een lijn (uniek)

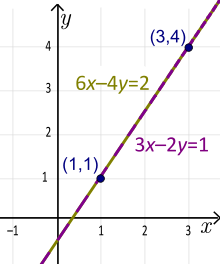
Standaardvorm van een lijn (niet uniek). De unieke hellingshoekvorm is y=1,5x-0,5

Afgeleide van een lineaire functie

In de context waarin hij is gedefinieerd, is de afgeleide van een functie een maat voor de mate van verandering van functiewaarden ten opzichte van veranderingen in invoerwaarden. Een lineaire functie heeft een constante veranderingssnelheid. Deze veranderingssnelheid is de helling m. Dus m is de afgeleide. Dit wordt vaak geschreven:

( m x + b ) ′ = m {displaystyle (mx+b)^{prime }=m} $(mx+b)^{\prime }=m$

Voorbeeld: y= -2x+4. Hier is m= -2 en dus y′= -2.

Lineaire functie vs. Lineaire vergelijking

Vaak worden de termen lineaire vergelijking en lineaire functie verward. Beide zijn veeltermen. Het woord lineair in lineaire vergelijking betekent echter dat alle termen met variabelen eerste graad zijn. (Een lineaire vergelijking kan 1, 2, 3 of meer variabelen hebben. Een lineaire vergelijking is dus alleen een lineaire functie als ze precies 2 variabelen heeft. (Een lineaire vergelijking in één variabele is een punt op de getallenlijn en een lineaire vergelijking in 3 variabelen is een vlak in de driedimensionale ruimte).

Notatie

Veel landen en disciplines gebruiken verschillende letters en volgorde voor de verschillende vormen.

In veel landen wordt een lineaire functie vaak geschreven als y = a x + b {\displaystyle y=ax+b} $y=ax+b$ waarbij a de helling is en b het y-intercept.

In het bedrijfsleven en de economie wordt een lineaire functie vaak geschreven als y = a + b x {\displaystyle y=a+bx} $y=a+bx$ waarbij a het y-intercept is en b de helling.

Verwante pagina's

Lijn
Polynoom
Constante functie
Kwadratische vergelijking
Lineaire vergelijking