Inwendig product

In de wiskunde is het scalair product een bewerking die twee vectoren als invoer neemt, en die een scalair getal als uitvoer geeft. Het teruggegeven getal is afhankelijk van de lengte van beide vectoren, en van de hoek tussen beide. De naam is afgeleid van de gecentreerde punt "-" die vaak gebruikt wordt om deze bewerking aan te duiden; de alternatieve naam scalair product benadrukt het scalaire (eerder dan vector) karakter van het resultaat.

Het scalair product staat (in de driedimensionale ruimte) in contrast met het scalair product, dat een vector als resultaat heeft.

Definitie

Het scalair product van twee vectoren a = [a1, a2, ..., an] en b = [b1, b2, ..., bn] is gedefinieerd als:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

waarbij Σ staat voor sommatie ( de som van alle termen) en n voor de dimensie van de vectorruimte.

In dimensie 2 is het scalair product van de vectoren [a,b] en [c,d] ac + bd. Op dezelfde manier is in dimensie 3 het scalair product van de vectoren [a,b,c] en [d,e,f] ad + be + cf. Bijvoorbeeld, het scalair product van twee drie-dimensionale vectoren [1, 3, -5] en [4, -2, -1] is

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( - 5 ) × ( - 1 ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {Stijl [1,3,-5]\cdot [4,-2,-1]=(1 keer 4)+(3 keer (-2))+((-5)\(-1)=(4)-(6)+(5)=3.} {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geometrische interpretatie

In de euclidische meetkunde zijn het scalair product, de lengte en de hoek met elkaar verwant. Voor een vector a is het scalair product a - a het kwadraat van de lengte van a, of

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=-links {mathbf {a} \right}}^{2}} {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

waarbij ||a| de lengte (magnitude) van a. aangeeft. Meer in het algemeen, als b een andere vector is

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} = \left\mathbf {a} \right\|,\left\mathbf {b} = links} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,}

waarbij ||a| en ||b| de lengte van a en b aanduiden en θ de hoek tussen beide is.

Deze formule kan herschikt worden om de grootte van de hoek tussen twee niet nul vectoren te bepalen:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}}{\dot {\mathbf {b}}}{\left}{\{\mathbf {b}}}}}}{\left}{\{\mathbf {b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}? {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Men kan ook eerst de vectoren omzetten in eenheidsvectoren door te delen door hun magnitude:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {a}}={\frac {\mathbf {a}}{\left}{\mathbf {a}}}right}}} {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

dan wordt de hoek θ gegeven door

θ = arccos ( a ^ ⋅ b ^ ) {Stijl \theta = arccos({\boldsymbol {\hat {a}}}} {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})}

Aangezien de cosinus van 90° nul is, is het scalair product van twee loodrecht op elkaar staande vectoren altijd nul. Bovendien kunnen twee vectoren als orthogonaal worden beschouwd als en slechts als hun scalair product nul is, en zij beide een lengte hebben die niet nul is. Deze eigenschap biedt een eenvoudige methode om de voorwaarde van orthogonaliteit te testen.

Soms worden deze eigenschappen ook gebruikt voor de definitie van het scalair product, vooral in 2 en 3 dimensies; deze definitie is gelijkwaardig aan de bovenstaande. Voor hogere dimensies kan de formule gebruikt worden om het begrip hoek te definiëren.

De geometrische eigenschappen berusten op het feit dat de basis orthonormaal is, d.w.z. samengesteld uit paarsgewijs loodrecht op elkaar staande vectoren met een lengte-eenheid.

Scalaire projectie

Als a en b beide lengte 1 hebben (d.w.z. eenheidsvectoren zijn), dan geeft hun scalair product eenvoudigweg de cosinus van de hoek tussen beide.

Als alleen b een eenheidsvector is, dan geeft het scalair product a - b |a| cos(θ), d.w.z. de grootte van de projectie van a in de richting van b, met een minteken als de richting tegengesteld is. Dit heet de scalaire projectie van a op b, of de scalaire component van a in de richting van b (zie figuur). Deze eigenschap van het scalair product heeft verschillende nuttige toepassingen (zie bijvoorbeeld volgende sectie).

Als noch a noch b een eenheidsvector is, dan is de grootte van de projectie van a in de richting van b bijvoorbeeld a - (b / |b|), want de eenheidsvector in de richting van b is b / |b|.

Rotatie

Een rotatie van de orthonormale basis waarin de vector a is voorgesteld, wordt verkregen door vermenigvuldiging van a met een rotatiematrix R. Deze matrixvermenigvuldiging is slechts een compacte weergave van een opeenvolging van dotproducten.

Bijvoorbeeld, laat

  • B1 = {x, y, z} en B2 = {u, v, w} zijn twee verschillende orthonormale grondslagen van dezelfde ruimte R3, waarbij B2 wordt verkregen door B1 enkel te roteren,
  • a1 = (ax, ay, az) stelt vector a voor in termen van B1,
  • a2 = (au, av, aw) stellen dezelfde vector voor in termen van de geroteerde basis B2,
  • u1, v1, w1 de geroteerde basisvectoren u, v, w zijn, voorgesteld in termen van B1.

Vervolgens wordt de draaiing van B1 naar B2 als volgt uitgevoerd:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf  } {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.}

Merk op dat de rotatiematrix R wordt samengesteld door de geroteerde basisvectoren u1, v1, w1 als zijn rijen te gebruiken, en deze vectoren zijn eenheidsvectoren. Per definitie bestaat Ra1 uit een opeenvolging van puntproducten tussen elk van de drie rijen van R en de vector a1. Elk van deze dotproducten bepaalt een scalaire component van a in de richting van een geroteerde basisvector (zie vorige sectie).

Indien a1 een rijvector is, in plaats van een kolomvector, dan moet R de geroteerde basisvectoren in zijn kolommen bevatten, en moet a1 post-multipliceren:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}}end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}}}{1}}&{\mathbf {a}}_{1}}&{1}}}&{1}}}&{1}}}{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.}

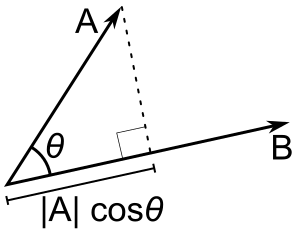
A - B = |A| |B| cos(θ). |A| cos(θ) is de scalaire projectie van A op B.Zoom
A - B = |A| |B| cos(θ). |A| cos(θ) is de scalaire projectie van A op B.

Natuurkunde

In de natuurkunde is de magnitude een scalair in de natuurkundige betekenis, d.w.z. een natuurkundige grootheid die onafhankelijk is van het coördinatenstelsel, uitgedrukt als het product van een getalswaarde en een natuurkundige eenheid, niet alleen een getal. Het scalair product is ook een scalair product in deze zin, gegeven door de formule, onafhankelijk van het coordinatensysteem. Voorbeeld:

Eigenschappen

De volgende eigenschappen gelden indien a, b, en c reele vectoren zijn en r een scalair is.

Het scalair product is commutatief:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =mathbf {b} = {mathbf {b} = {mathbf {b} } {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .}

Het scalair product is distributief over vector optelling:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} + {mathbf {a} \cdot {mathbf {c} . } {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}

Het scalair product is bilineair:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).}

Wanneer vermenigvuldigd met een scalaire waarde, voldoet dot product:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(deze laatste twee eigenschappen volgen uit de eerste twee).

Twee vectoren a en b, niet nul, staan loodrecht op elkaar als en slechts als a - b = 0.

In tegenstelling tot vermenigvuldiging van gewone getallen, waarbij als ab = ac, dan is b altijd gelijk aan c tenzij a nul is, gehoorzaamt het scalair product niet aan de annuleringswet:

Als a - b = a - c en a ≠ 0, dan kunnen we schrijven: a - (b - c) = 0 door de distributieve wet; het resultaat hierboven zegt alleen dat a loodrecht staat op (b - c), waardoor (b - c) ≠ 0, en dus b ≠ c nog steeds mogelijk is.

Op voorwaarde dat de basis orthonormaal is, is het scalair product invariant onder isometrische veranderingen van de basis: rotaties, spiegelingen, en combinaties, waarbij de oorsprong vast blijft. De bovenvermelde meetkundige interpretatie berust op deze eigenschap. Met andere woorden, voor een orthonormale ruimte met een willekeurig aantal dimensies, is het scalair product invariant onder een coördinatentransformatie gebaseerd op een orthogonale matrix. Dit komt overeen met de volgende twee voorwaarden:

  • De nieuwe basis is weer orthonormaal (d.w.z. orthonormaal uitgedrukt in de oude basis).
  • De nieuwe basisvectoren hebben dezelfde lengte als de oude (d.w.z. eenheidslengte in termen van de oude basis).

Als a en b functies zijn, dan is de afgeleide van a - b a' - b + a - b'

Drievoudige product uitbreiding

Dit is een zeer nuttige identiteit (ook bekend als de formule van Lagrange) waarbij de punt- en nevenproducten betrokken zijn. Ze wordt geschreven als

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

die gemakkelijker te onthouden is als "BAC min CAB", waarbij in gedachten moet worden gehouden welke vectoren met elkaar zijn verbonden. Deze formule wordt vaak gebruikt om vectorberekeningen in de natuurkunde te vereenvoudigen.

Bewijs van de geometrische interpretatie

Beschouw het element van Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Herhaalde toepassing van de stelling van Pythagoras geeft voor de lengte |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {Displaystyle |mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Maar dit is hetzelfde als

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

dus concluderen we dat het nemen van het scalair product van een vector v met zichzelf de gekwadrateerde lengte van de vector oplevert.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Beschouw nu twee vectoren a en b, uitgaande van de oorsprong, gescheiden door een hoek θ. Een derde vector c kan gedefinieerd worden als

c = d e f a - b . {\displaystyle \mathbf {c} \stackrel {\mathrm {def} }{=}} {\mathbf {a} -\mathbf {b} .\,} {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,}

een driehoek vormen met zijden a, b, en c. Volgens de wet van cosinussen, hebben we

c 2 = a 2 + b 2 - 2 a b cos θ . {\displaystyle |\mathbf {c} |^{2}=|Mathbf {a} |^{2}+|mathbf {b} |^{2}-2|mathbf {a} . Theta.} {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Als we de gekwadrateerde lengtes substitueren door puntproducten volgens Lemma 1, krijgen we

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} = {mathbf {a} \cdot \mathbf {a} +\mathbf {b} -2 |mathbf {b} (1){\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Maar aangezien c ≡ a - b, hebben we ook

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,}{\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

die, volgens de distributieve wet, uitbreidt tot

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} = {mathbf {a} \cdot \mathbf {a} +\mathbf {b} \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).} {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,}(2)

Als we de twee c - c vergelijkingen, (1) en (2), samenvoegen, bekomen we

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . \displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} = -2%mathbf {a} = -2%mathbf {a} = -2%mathbf {b} = -2%mathbf {a} = -2%mathbf {b} |mathbf {b} .} {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Door a - a + b - b van beide kanten af te trekken en te delen door -2 blijft over

a ⋅ b = | a | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} | |mathbf {b} |theta .} {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalisatie

Het inwendig product veralgemeent het scalair product tot abstracte vectorruimten en wordt gewoonlijk aangeduid met ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \hoekle } {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle }. Door de meetkundige interpretatie van het scalair product is de norm ||a|| van een vector a in zo'n binnenproductruimte gedefinieerd als

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }} {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

zodat het de lengte veralgemeent, en de hoek θ tussen twee vectoren a en b door

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . . vlakle }{\\\mathbf {a} \,\\\mathbf {b} \|}}. } {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.}

In het bijzonder worden twee vectoren als orthogonaal beschouwd als hun inwendig product nul is

⟨ a , b ⟩ = 0. {\an5} \mathbf {a} \hoekle =0.} {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Voor vectoren met complexe ingangen zou het gebruik van de gegeven definitie van het scalair product tot heel andere meetkundige eigenschappen leiden. Zo kan het scalair product van een vector met zichzelf een willekeurig complex getal zijn, en kan het nul zijn zonder dat de vector de nulvector is; dit zou op zijn beurt ernstige gevolgen hebben voor begrippen als lengte en hoek. Veel meetkundige eigenschappen kunnen worden gered, ten koste van het opgeven van de symmetrische en bilineaire eigenschappen van het scalair product, door als alternatief te definiëren

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =sum {a_{i}{\overline {b_{i}}}}} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

waarbij bi het complex conjugaat van bi is. Dan is het scalair product van een willekeurige vector met zichzelf een niet-negatief reeel getal, en het is niet nul behalve voor de nulvector. Dit scalair product is echter niet lineair in b (maar eerder geconjugeerd lineair), en het scalair product is ook niet symmetrisch, want

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a}} }}} {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}.

Dit type scalair product is niettemin zeer nuttig, en leidt tot de begrippen Hermitische vorm en algemene binnenproductruimten.

Het inwendig product van Frobenius veralgemeent het scalair product naar matrices. Het is gedefinieerd als de som van de producten van de overeenkomstige componenten van twee matrices van dezelfde grootte.

Generalisatie naar tensoren

Het scalair product tussen een tensor van orde n en een tensor van orde m is een tensor van orde n+m-2. Het scalair product wordt verkregen door vermenigvuldiging en sommatie over een enkele index in beide tensoren. Als A {{A}} en B {{A}}} } {\displaystyle \mathbf {A} }en B {\displaystyle \mathbf {B}} }{\displaystyle \mathbf {B} } twee tensoren zijn met elementvoorstelling A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\dots }} {\displaystyle A_{ij\dots }^{k\ell \dots }}en B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} {\displaystyle B_{mn\dots }^{p{\dots }i}}de elementen van het scalair product A ⋅ B {\displaystyle \mathbf {A}} \dot \mathbf {B}} {\displaystyle \mathbf {A} \cdot \mathbf {B} }zijn gegeven door

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {Displaystyle A_{ij\dots }^{kell \dots }B_{mn\dots }^{p{\dots }i}=sum _{i=1}^{n}A_{ij\dots }^{kell \dots }B_{mn\dots }^{p{\dots }i} {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Deze definitie herleidt natuurlijk tot het standaard vectordotproduct bij toepassing op vectoren, en tot matrixvermenigvuldiging bij toepassing op matrices.

Soms wordt een dubbel scalair product gebruikt om vermenigvuldigen en optellen over twee indices weer te geven. Het dubbele scalair product tussen twee 2e orde tensoren is een scalair.

Verwante pagina's

 

Vragen en antwoorden

V: Wat is het scalair product in de wiskunde?


A: Het scalair product is een bewerking die twee vectoren als invoer neemt en een scalair getal als uitvoer geeft.

V: Waar hangt het product van af?


A: Het scalair product hangt af van de lengte van beide vectoren en van de hoek tussen beide vectoren.

V: Waarom is de naam van het scalair product afgeleid van de gecentreerde punt "-"?


A: De naam is afgeleid van de gecentreerde punt "-" die vaak wordt gebruikt om deze bewerking aan te duiden.

V: Wat is de alternatieve naam voor het scalair product?


A: De alternatieve naam is scalair product, wat de scalaire (in plaats van vector) aard van het resultaat benadrukt.

Vraag: Wat is het verschil tussen het product van de punt en het product van het kruis in de driedimensionale ruimte?


Antwoord: Het scalair product geeft een scalair getal als resultaat, terwijl het kruisproduct een vector als resultaat geeft.

V: Waar wordt het product van de punt voor gebruikt in de wiskunde?


A: Het scalair product kan gebruikt worden om te bepalen of twee vectoren loodrecht op elkaar staan (een hoek van 90 graden hebben) en om een vector op een andere te projecteren.

V: Kan het scalair product gebruikt worden in ruimten met hogere dimensies?


A: Ja, het scalair product kan worden uitgebreid naar ruimten van hogere dimensies door de definitie te veralgemenen.

AlegsaOnline.com - 2020 / 2023 - License CC3