Elektromagnetische straling

Elektromagnetische golven zijn golven die een elektrisch veld en een magnetisch veld bevatten en energie dragen. Ze reizen met de snelheid van het licht.

Quantummechanica ontwikkeld uit de studie van elektromagnetische golven. Dit veld omvat de studie van zowel zichtbaar als onzichtbaar licht. Zichtbaar licht is het licht dat men met normaal gezichtsvermogen kan zien in de kleuren van de regenboog. Onzichtbaar licht is het licht dat men niet kan zien met normaal gezichtsvermogen en omvat meer energetische en hoger frequente golven, zoals ultraviolet, röntgenstraling en gammastralen. Golven met een langere lengte, zoals infrarood, micro en radiogolven, worden ook onderzocht op het gebied van de kwantummechanica.

Sommige soorten elektromagnetische straling, zoals röntgenstraling, zijn ioniserende straling en kunnen schadelijk zijn voor het lichaam. Ultraviolette stralen bevinden zich aan het violette uiteinde van het lichtspectrum en infrarood aan het rode uiteinde. Infraroodstralen zijn warmtestralen en ultraviolette stralen veroorzaken zonnebrand.

De verschillende delen van het elektromagnetisch spectrum verschillen in golflengte, frequentie en kwantumenergie.

Geluidsgolven zijn geen elektromagnetische golven, maar drukgolven in lucht, water of een andere stof.

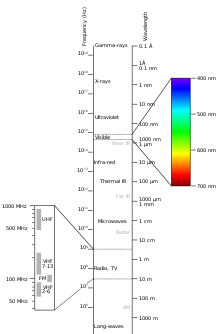
Het bereik van de elektromagnetische frequenties. "UHF" betekent "ultra hoge frequentie," VHF is "zeer hoge frequentie". Beide werden vroeger gebruikt voor televisie in de VS.

Wiskundige formulering

In de natuurkunde is het bekend dat de golfvergelijking voor een typische golf

∇ 2 f = 1 c 2 ∂ 2 f ∂ t 2 {\\\nabla ^2}f={frac {c^2}}}{frac {partieel ^2}f}{partieel ^2}}}} $\nabla ^{2}f={\frac {1}{c^{2}}}{\frac {\partial ^{2}f}{\partial t^{2}}}$

Het probleem is nu om te bewijzen dat de vergelijkingen van Maxwell expliciet bewijzen dat de elektrische en magnetische velden elektromagnetische straling creëren. Bedenk dat twee van Maxwell's vergelijkingen worden gegeven door

∇ × E = - ∂ B ∂ t t tuurlijk is de nablaistische manier van spelen... {\\\an5} $\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

∇ × B = μ o j + μ o ϵ o ∂ E ∂ t t t e e r v a n d e m a a t r e g e l e n v a n m a t r e g e l e n v a n m a t r e g e l e n v a n m a t r e g e l e n v a n m a t r e g e l e n v a n m a t r e g e l e n . +\Ik heb de hele dag door een paar dagen geleden... {\\\an5} $\nabla \times \mathbf {B} =\mu _{o}\mathbf {j} +\mu _{o}\epsilon _{o}{\frac {\partial \mathbf {E} }{\partial t}}$

Door het evalueren van de krul van bovenstaande vergelijkingen en vectorrekening kan men de volgende vergelijkingen bewijzen

∇ 2 E = 1 c 2 ∂ 2 E ∂ t {\\\\nabla {2}mathbf {E} ={frac {c {2}}}{frac {partieel {2}mathbf {E}} {\\\an5} $\nabla ^{2}\mathbf {E} ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t}}$

∇ 2 B = 1 c 2 ∂ 2 B ∂ t t t.o.v. de nabla {2}mathbf {B} ={frac {c {2}} {frac {partieel {2}mathbf {B}}. {\\\an5} $\nabla ^{2}\mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t}}$

Opmerking: het bewijs bestaat uit het maken van de vervanging

c = 1 μ o ϵ {\frac {1}{\frac {mu _o}epsilon }}}} $c={\frac {1}{\sqrt {\mu _{o}\epsilon }}}$

De bovenstaande vergelijkingen zijn analoog aan de golfvergelijking, door f te vervangen door E en B. De bovenstaande vergelijkingen betekenen dat propagaties door de magnetische (B) en elektrische (E) velden golven zullen produceren.

Gerelateerde pagina's

Foton

Vragen en antwoorden

V: Wat zijn elektromagnetische golven?

A: Elektromagnetische golven zijn golven die een elektrisch veld en een magnetisch veld bevatten en energie dragen. Zij verplaatsen zich met de lichtsnelheid (299.792.458 meter per seconde).

V: Wat is kwantummechanica?

A: Kwantummechanica is een studiegebied dat zich heeft ontwikkeld uit de studie van elektromagnetische golven. Het omvat de studie van zowel zichtbaar als onzichtbaar licht.

V: Welke soorten elektromagnetische straling kunnen schadelijk zijn voor uw lichaam?

A: Sommige soorten elektromagnetische straling, zoals röntgenstraling, zijn ioniserende straling en kunnen schadelijk zijn voor uw lichaam.

V: Waar vallen ultraviolette stralen in het lichtspectrum?

A: Ultraviolette stralen bevinden zich dicht bij het violette uiteinde van het lichtspectrum.

V: Waar vallen infrarode stralen in het lichtspectrum?

A: Infraroodstralen bevinden zich aan de rode kant van het lichtspectrum.

V: Waarin verschillen infrarode stralen van ultraviolette stralen?

A: Infraroodstralen worden gebruikt als warmtestralen en ultraviolette stralen veroorzaken zonnebrand.

V: Worden geluidsgolven beschouwd als elektromagnetische golven?

A: Nee, geluidsgolven zijn geen elektromagnetische golven, maar eerder drukgolven in lucht, water of een andere stof.