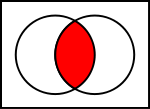
Venndiagram | diagram dat de logische relatie tussen sets weergeeft

Een Venn-diagram is een diagram dat de logische relatie tussen verzamelingen weergeeft. Ze werden in de jaren 1880 populair gemaakt door John Venn, en worden nu veel gebruikt. Ze worden gebruikt om elementaire verzamelingenleer te onderwijzen en om eenvoudige relaties tussen verzamelingen te illustreren in waarschijnlijkheid, logica, statistiek, taalkunde en informatica. Een Venn-diagram maakt gebruik van gesloten krommen op een vlak om verzamelingen voor te stellen. Vaak zijn deze krommen cirkels of ellipsen.

Soortgelijke ideeën waren al vóór Venn voorgesteld. Zo kwamen Christian Weise in 1712 (Nucleus Logicoe Wiesianoe) en Leonhard Euler (Brieven aan een Duitse prinses) in 1768 met soortgelijke ideeën. Het idee werd gepopulariseerd door Venn in Symbolic Logic, Chapter V "Diagrammatic Representation", 1881.

Gebrandschilderd raam in Cambridge, waar John Venn studeerde. Het toont een Venn-diagram.

Voorbeeld

In het volgende voorbeeld worden twee groepen gebruikt, A en B, hier weergegeven als gekleurde cirkels. De oranje cirkel, set A, staat voor alle levende wezens die tweebenig zijn. De blauwe cirkel, reeks B, vertegenwoordigt de levende wezens die kunnen vliegen. Elk afzonderlijk type wezen kan worden voorgesteld als een punt ergens in het diagram. Levende wezens die zowel kunnen vliegen als twee benen hebben - bijvoorbeeld papegaaien - zitten dan in beide groepen, en komen dus overeen met punten in het gebied waar de blauwe en oranje cirkels elkaar overlappen. Dat gebied bevat alle (en alleen) dergelijke levende wezens.

Mensen en pinguïns zijn tweevoetig, en staan dus in de oranje cirkel, maar omdat ze niet kunnen vliegen, staan ze in het linkerdeel van de oranje cirkel, waar die niet overlapt met de blauwe cirkel. Muggen hebben zes poten, en vliegen, dus het punt voor muggen ligt in het deel van de blauwe cirkel dat niet overlapt met de oranje cirkel. Wezens die niet tweebenig zijn en niet kunnen vliegen (bijvoorbeeld walvissen en spinnen) zouden allemaal worden voorgesteld door punten buiten beide cirkels.

De gecombineerde oppervlakte van de verzamelingen A en B wordt de unie van A en B genoemd, aangeduid met A ∪ B. De unie bevat in dit geval alle levende wezens die hetzij tweebenig zijn, hetzij kunnen vliegen (of beide). Het gebied in zowel A als B, waar de twee verzamelingen elkaar overlappen, wordt het snijpunt van A en B genoemd, aangeduid met A ∩ B. Het snijpunt van de twee verzamelingen is bijvoorbeeld niet leeg, omdat er punten zijn die wezens voorstellen die zowel in de oranje als de blauwe cirkel zitten.

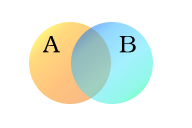
Sets A (wezens met twee benen) en B (wezens die kunnen vliegen)

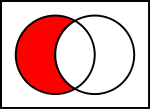
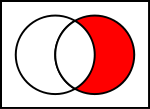
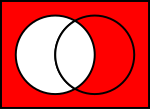
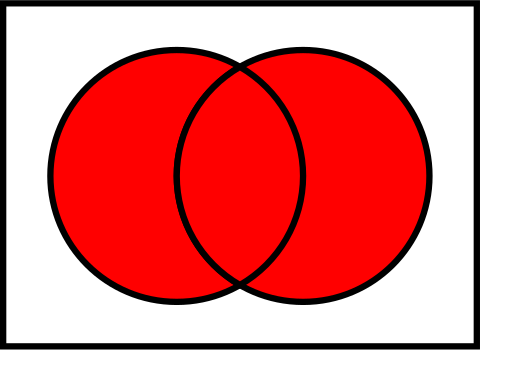
Venn-diagrammen van gemeenschappelijke operaties op verzamelingen

In de onderstaande illustraties toont de linkercirkel set A {displaystyle A} $A$ en de rechtercirkel set B {displaystyle B} $B$ . De resultaten van de bewerkingen worden weergegeven als gekleurde gebieden.

Verschil A ∖ B {afbeelding A min B} $A\setminus B$

Verschil B ∖ A {afbeelding B min A} $B\setminus A$

Complement van A A C = U ∖ A {Displaystyle A^{{rm {C}}=U}setminus A} $A^{\rm {C}}=U\setminus A$

Unie A ∪ B {Displaystyle B} $A\cup B$

Snijpunt A ∩ B $A\cap B$

Gerelateerde pagina's

Exclusieve scheiding
Inclusieve loskoppeling

Vragen en antwoorden

V: Wat is een Venn-diagram?

A: Een Venn-diagram is een diagram dat de logische relatie tussen verzamelingen weergeeft. Het gebruikt gesloten krommen die op een vlak zijn getekend, meestal cirkels of ellipsen, om verzamelingen voor te stellen.

V: Wie heeft Venn-diagrammen populair gemaakt?

A: John Venn maakte Venn-diagrammen populair in de jaren 1880.

V: Waarvoor worden ze gebruikt?

A: Ze worden gebruikt om elementaire verzamelingenleer te onderwijzen en eenvoudige relaties tussen verzamelingen te illustreren in waarschijnlijkheid, logica, statistiek, taalkunde en informatica.

V: Wie stelde vóór John Venn soortgelijke ideeën voor?

A: Christian Weise stelde soortgelijke ideeën voor in 1712 met zijn Nucleus Logicoe Wiesianoe en Leonhard Euler stelde ze voor in Brieven aan een Duitse prinses in 1768.

V: Wanneer publiceerde John Venn de Symbolische Logica?

A: John Venn publiceerde Symbolic Logic in 1881.

V: In welk hoofdstuk van Symbolic Logic werd het idee van een Venn-diagram door John Venn gepopulariseerd?

A: Het idee van een Venn-diagram werd gepopulariseerd door John Venn in hoofdstuk 5 "Diagrammatic Representation" van Symbolic Logic.

V: Hoe werden deze ideeën weergegeven vóór de uitvinding van de moderne versie van het Venn-diagram?

A: Vóór de uitvinding van de hedendaagse versie van het V enn-diagram werden deze ideeën voorgesteld met behulp van gesloten krommen die op een vlak werden getekend, zoals cirkels of ellipsen.