Harmonische rij

In de wiskunde is de harmonische reeks de divergente oneindige reeks:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {{{n=1}^{{frac {1}{n}}=1+{{frac {1}{2}}+{{frac {1}{3}}+{{frac {1}{4}}+{{frac {1}{5}}+{cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergent betekent dat wanneer u meer termen toevoegt, de som steeds groter wordt. Het gaat niet naar één eindige waarde.

Oneindig betekent dat u altijd nog een term kunt toevoegen. De reeks heeft geen eindterm.

De naam komt van het idee van harmonischen in de muziek: de golflengte van de boventonen van een trillende snaar is 1/2,

1/3, 1/4, enz. van de fundamentele golflengte van de snaar. Behalve de eerste term is elke term van de reeks het harmonisch gemiddelde van de termen ernaast. De uitdrukking harmonisch gemiddelde komt ook uit de muziek.

Geschiedenis

Het feit dat de harmonische reeks divergeert werd voor het eerst bewezen in de 14e eeuw door Nicole Oresme, maar raakte in de vergetelheid. Bewijzen werden in de 17e eeuw gegeven door Pietro Mengoli, Johann Bernoulli en Jacob Bernoulli.

Harmonische reeksen zijn gebruikt door architecten. In de barokperiode gebruikten architecten ze in de verhoudingen van plattegronden, verhogingen en in de relaties tussen architectonische details van kerken en paleizen.

Divergentie

Er zijn verschillende bekende bewijzen van de divergentie van de harmonische reeks. Hieronder volgen er enkele.

Vergelijkingstest

Eén manier om divergentie aan te tonen is de harmonische reeks te vergelijken met een andere divergente reeks, waarbij elke noemer wordt vervangen door de op één na grootste macht van twee:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {{\displaystyle {begin{aligned}&{}1+{{frac {1}{2}}+{{frac {1}{3}}+{{frac {1}{4}}+{{frac {1}{5}}+{frac {1}{6}}+{{frac {1}{7}}+{frac {1}{8}+{frac {1}{9}}+{cdots \geq {}&...1+{{{frac {1}{2}}+{{{frac {1}{{{{{{{{=rood}}{{=mathbf {4}} }}+{{frac {1}{4}}+{{frac {1}{{{{{{{=rode}{{=mathbf {8}} }}+{{frac {1}{{{{rood}{{{{mathbf {8}} }}+{{frac {1}{{collor {red}{{mathbf {8}}} }}+{{frac {1}{8}}+{{frac {1}{{{{{{{=color {red}{{=mathbf {16}}} }}+{ccdots {aligned}}}. ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Elke term van de harmonische reeks is groter of gelijk aan de overeenkomstige term van de tweede reeks, en daarom moet de som van de harmonische reeks groter of gelijk zijn aan de som van de tweede reeks. De som van de tweede reeks is echter oneindig:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {begin{aligned}&{}1+links({1}{2}}) +links({1}{4}}!+links({1}{4}} rechts)+links({1}{8}}!+{1}{8}}! +{1}{8}}! +{1}{8}}! +{1}{8}} rechts)+{1}{16}}!{\frac {1}{16}} rechts)+\cdots \[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\infty \end{aligned}}}. ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Hieruit volgt (door de vergelijkingstest) dat de som van de harmonische reeksen ook oneindig moet zijn. Meer precies bewijst bovenstaande vergelijking dat

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{{frac {1}{n}}geq 1+{{frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

voor elk positief geheel getal $k$ .

Dit bewijs, voorgesteld door Nicole Oresme rond 1350, wordt beschouwd als een hoogtepunt van de middeleeuwse wiskunde. Het is vandaag de dag nog steeds een standaardbewijs dat in wiskundecolleges wordt onderwezen.

Integrale test

Het is mogelijk te bewijzen dat de harmonische reeks divergeert door de som ervan te vergelijken met een oneigenlijke integraal. Beschouw de opstelling van rechthoeken in de figuur hiernaast. Elke rechthoek is 1 eenheid breed en

1/n eenheden hoog, dus de totale oppervlakte van het oneindig aantal rechthoeken is de som van de harmonische reeksen:

oppervlakte van rechthoeken = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {{displaystyle}{c}{{tekst{gebied van}}{{tekst{rechthoeken}}{end{array}}=1+{{frac {1}{2}}+{{frac {1}{3}}+{{frac {1}{4}}+{frac {1}{5}}+{cdots}}. ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

De totale oppervlakte onder de kromme $y =$

1/x van 1 tot oneindig wordt gegeven door een divergerende oneigenlijke integraal:

oppervlakte onder de curve = ∫ 1 ∞ 1 x d x = ∞ . {displaystyle {begin{array}{c}{text{area under}}{{curve}}{end{array}}=int _{1}^{infty }{frac {1}{x}}, dx=infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Aangezien deze oppervlakte volledig binnen de rechthoeken valt, moet de totale oppervlakte van de rechthoeken ook oneindig zijn. Dit bewijst dat

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{{frac {1}{n}}>\int _{1}^{k+1}{{frac {1}{x}},dx= ln ( k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

De veralgemening van dit argument staat bekend als de integrale toets.

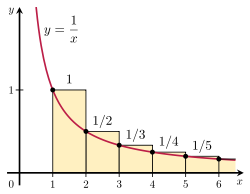
Illustratie van de integrale test.

Mate van divergentie

De harmonische reeks divergeert zeer langzaam. De som van de eerste 10 termen van⁴³ is bijvoorbeeld minder dan 100. Dit komt omdat de deelsommen van de reeks logaritmisch groeien. In het bijzonder,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle sum _{n=1}^{k}{frac {1}{n}}={ln k+\gamma +{varepsilon _{k}\leq (\ln k)+1}} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

waarbij γ de Euler-Mascheroni constante is en $ε k ~$

1/2k die 0 benadert als $k$ naar oneindig gaat. Leonhard Euler bewees zowel dit als dat de som die alleen de reciprocalen van priemgetallen omvat ook divergeert, dat wil zeggen:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{priem}}{{frac {1}{p}}={{frac {1}{2}}+{{frac {1}{3}}+{frac {1}{5}}+{frac {1}{7}}+{frac {1}{11}}+{{frac {1}{13}}+{frac {1}{17}}}+{cdots =\infty .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Gedeeltelijke sommen

De eerste dertig harmonische getallen
$n$	Gedeeltelijke som van de harmonische reeks, $H n$
$n$	uitgedrukt als fractie		decimaal	relatieve grootte
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

De eindige partiële sommen van de divergerende harmonische reeksen,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=sum _{k=1}^{n}{frac {1}{k}},}. $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

worden harmonische getallen genoemd.

Het verschil tussen $H n$ en $ln n$ convergeert naar de Euler-Mascheroni constante. Het verschil tussen twee harmonische getallen is nooit een geheel getal. Geen enkel harmonisch getal is een geheel getal, behalve $H 1 = 1$ .

Verwante series

Afwisselende harmonische reeks

De serie

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {{displaystyle \sum _{n=1}^{{infty }{{frac {(-1)^{n+1}}{n}}=1-{frac {1}{2}}+{{frac {1}{3}}-{frac {1}{4}}+{frac {1}{5}}-{cdots }. $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

staat bekend als de alternerende harmonische reeks. Deze reeks convergeert volgens de alternerende reekstest. In het bijzonder is de som gelijk aan de natuurlijke logaritme van 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{{frac {1}{2}}+{{frac {1}{3}}-{{frac {1}{4}}+{{frac {1}{5}}-\dots = ln 2.}. $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

De afwisselende harmonische reeks is weliswaar voorwaardelijk convergerend, maar niet absoluut convergerend: als de termen in de reeks systematisch worden herschikt, wordt de som in het algemeen anders en, afhankelijk van de herschikking, mogelijk zelfs oneindig.

De formule van de alternerende harmonische reeks is een speciaal geval van de Mercator-reeks, de Taylor-reeks voor de natuurlijke logaritme.

Een verwante reeks kan worden afgeleid uit de Taylorreeks voor de arctangens:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{{frac {(-1)^{n}}{2n+1}}=1-{frac {1}{3}}+{frac {1}{5}}-{frac {1}{7}}+{frac {pi }{4}}. $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Dit staat bekend als de Leibniz-reeks.

Algemene harmonische reeksen

De algemene harmonische reeks is van de vorm

∑ n = 0 ∞ 1 a n + b , {\displaystyle sum _{n=0}^{infty }{frac {1}{an+b}},}. $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

waarbij $a \neq 0$ en $b$ reële getallen zijn, en

b/a is niet nul of een negatief geheel getal.

Door de limietvergelijkingstest met de harmonische reeksen divergeren alle algemene harmonische reeksen ook.

$p-serie$

Een veralgemening van de harmonische reeks is de $p-reeks$ (of hyperharmonische reeks), gedefinieerd als

∑ n = 1 ∞ 1 n p {{displaystyle \sum _{n=1}^{infty }{frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

voor elk reëel getal $p$ . Als $p = 1$ , is de $p-reeks$ de harmonische reeks, die divergeert. Uit de integraaltest of de condensatietest van Cauchy blijkt dat de $p-reeks$ voor alle $p > 1$ convergeert (in dat geval heet hij de over-harmonische reeks) en voor alle $p \leq 1$ divergeert. Als $p > 1$ dan is de som van de $p-reeksen$ ζ $(p)$ , d.w.z. de Riemann zetafunctie geëvalueerd op $p$ .

Het probleem van het vinden van de som voor $p = 2$ heet het Bazelse probleem; Leonhard Euler toonde aan dat het

$π$ ² /6. De waarde van de som voor $p = 3 wordt$ de constante van Apéry genoemd, omdat Roger Apéry heeft bewezen dat het een irrationeel getal is.

ln-reeks

Verwant aan de $p-reeks$ is de ln-reeks, gedefinieerd als

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle sum _{n=2}^{infty }{frac {1}{n(ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

voor elk positief reëel getal $p$ . Met de integrale test kan worden aangetoond dat deze divergeert voor $p \leq 1,$ maar convergeert voor alle $p > 1$ .

$φ-serie$

Voor elke convexe, reëel geaarde functie φ zodat

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u tot 0^{+}}{{frac {varphi \left({frac {u}{2}}}}<{frac {1}{2}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

de serie

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle sum _{n=1}^{infty } }varphi \left({frac {1}{n}}right) }. $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

is convergent.

Willekeurige harmonische reeks

De willekeurige harmonische reeks

∑ n = 1 ∞ s n n , {{n=1}^{infty }{frac {s_{n}}}{n}},}. $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

waarbij de $s n$ onafhankelijke, identiek verdeelde willekeurige variabelen zijn die met gelijke waarschijnlijkheid de waarden +1 en -1 aannemen.

1/2, is een bekend voorbeeld in de kansrekening voor een reeks willekeurige variabelen die met kans 1 convergeert. Het feit van deze convergentie is een eenvoudig gevolg van de stelling van Kolmogorov over drie reeksen of van de nauw verwante maximale ongelijkheid van Kolmogorov. Byron Schmuland van de Universiteit van Alberta onderzocht verder de eigenschappen van de willekeurige harmonische reeks, en toonde aan dat de convergente reeks een willekeurige variabele is met enkele interessante eigenschappen. In het bijzonder neemt de kansdichtheidsfunctie van deze willekeurige variabele geëvalueerd op +2 of op -2 de waarde 0,1249999999999999999999999999999999764... aan, die minder dan 10⁻⁴² afwijkt van 1/8 . Het artikel van Schmuland legt uit waarom deze kans zo dicht bij, maar niet precies, 1/8 ligt. De exacte waarde van deze kans wordt gegeven door het oneindige cosinusproduct integraal $C 2$ gedeeld door $π.$

Uitgeputte harmonische reeks

Er kan worden aangetoond dat de uitgeputte harmonische reeks waarin alle termen waarin het cijfer 9 ergens in de noemer voorkomt zijn verwijderd, convergeert en dat de waarde minder dan 80 is. In feite convergeert de reeks wanneer alle termen met een bepaalde reeks cijfers (in welke basis dan ook) worden verwijderd.

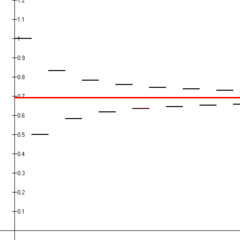
De eerste veertien partiële sommen van de afwisselende harmonische reeks (zwarte lijnstukken) convergeren naar de natuurlijke logaritme van 2 (rode lijn).

Toepassingen

De harmonische reeks kan contra-intuïtief zijn. Dat komt omdat het een divergente reeks is, ook al worden de termen van de reeks kleiner en gaan ze richting nul. De divergentie van de harmonische reeks is de bron van enkele paradoxen.

De "worm op het elastiek". Stel dat een worm langs een oneindig elastisch elastiek van een meter kruipt terwijl het elastiek gelijkmatig wordt uitgerekt. Als de worm 1 centimeter per minuut aflegt en het elastiek 1 meter per minuut uitrekt, zal de worm dan ooit het einde van het elastiek bereiken? Het antwoord is, contra-intuïtief, "ja", want na $n$ minuten is de verhouding tussen de door de worm afgelegde afstand en de totale lengte van het elastiekje

1 100 ∑ k = 1 n 1 k . {{k=1}^{n}{{frac {1}{100}}}. ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Omdat de reeks willekeurig groot wordt naarmate $n$ groter wordt, moet deze verhouding uiteindelijk groter zijn dan 1, wat betekent dat de worm het einde van het elastiek bereikt. De waarde van $n$ waarbij dit gebeurt, moet echter extreem groot zijn: ongeveer e $100$ , een getal van meer dan 10⁴³ minuten (10³⁷ jaar). De harmonische reeks divergeert weliswaar, maar zeer langzaam.

Het Jeep-probleem vraagt hoeveel totale brandstof nodig is voor een auto met een beperkte brandstofcapaciteit om een woestijn te doorkruisen, waarbij onderweg brandstofdruppels worden achtergelaten. De afstand die de auto kan afleggen met een gegeven hoeveelheid brandstof is gerelateerd aan de deelsommen van de harmonische reeks, die logaritmisch groeien. De benodigde brandstof neemt dus exponentieel toe met de gewenste afstand.

Het blokstapelprobleem: gegeven een verzameling identieke dominostenen is het mogelijk om ze aan de rand van een tafel te stapelen zodat ze over de rand van de tafel hangen zonder te vallen. Het contra-intuïtieve resultaat is dat ze kunnen worden gestapeld op een manier die de overhang zo groot maakt als u wilt. Tenminste, als er genoeg dominostenen zijn.

Een zwemmer die sneller gaat telkens hij de wand van het zwembad raakt. De zwemmer begint met een snelheid van 2 m/s over een bad van 10 meter, en bij elke oversteek wordt daar nog eens 2 m/s aan toegevoegd. In theorie is de snelheid van de zwemmer onbeperkt, maar het aantal keren dat hij het zwembad moet oversteken om die snelheid te bereiken wordt zeer groot; om bijvoorbeeld de lichtsnelheid te bereiken (zonder rekening te houden met speciale relativiteit) moet de zwemmer 150 miljoen keer het zwembad oversteken. In tegenstelling tot dit grote getal is de tijd die nodig is om een bepaalde snelheid te bereiken afhankelijk van de som van de reeksen bij een gegeven aantal zwembadovergangen:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}}sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Uit de berekening van de som blijkt dat de tijd die nodig is om de lichtsnelheid te bereiken slechts 97 seconden bedraagt.

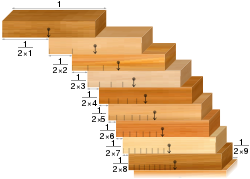
Het blokstapelprobleem: blokken uitgelijnd volgens de harmonische reeks overbrugt spleten van willekeurige breedte.

Gerelateerde pagina's

Harmonische progressie
Lijst van sommen van reciprocalen

Vragen en antwoorden

V: Wat is de harmonische reeks?

A: De harmonische reeks is een oneindige divergente reeks waarbij elke term gelijk is aan 1 gedeeld door zijn positie in de reeks.

V: Wat betekent het dat een reeks divergent is?

A: Divergent betekent dat als u meer termen toevoegt, de som steeds groter wordt en niet naar één eindige waarde toegaat.

V: Wat betekent dat een reeks oneindig is?

A: Oneindig betekent dat u altijd nog een term kunt toevoegen en dat de reeks geen eindterm heeft.

V: Waar komt de naam van deze reeks vandaan?

A: De naam van deze reeks komt van het idee van harmonischen in de muziek, waarbij de golflengten van boventonen 1/2, 1/3, 1/4, enz. zijn van de fundamentele golflengte van de snaar.

V: Wat is een harmonisch gemiddelde?

A: Een harmonisch gemiddelde is wanneer elke term in een reeks gelijk is aan het harmonisch gemiddelde van de naburige termen. Deze uitdrukking komt ook uit de muziek.

V: Hoe berekenen wij elke term in deze reeks?

Antwoord: Elke term in deze reeks kan worden berekend door één te delen door zijn positie in de reeks (1/n).