Taylorreeks
Een Taylorreeks is een idee dat wordt gebruikt in de informatica, calculus, scheikunde, natuurkunde en andere soorten wiskunde op hoger niveau. Het is een reeks die wordt gebruikt om een schatting (gok) te maken van hoe een functie eruit ziet. Er is ook een speciale soort Taylorreeks die Maclaurin-reeks wordt genoemd.
De theorie achter de Taylorreeks is dat als een punt wordt gekozen op het coördinatenvlak (x- en y-as), het mogelijk is te raden hoe een functie eruit zal zien in het gebied rond dat punt. Dit wordt gedaan door de afgeleiden van de functie te nemen en deze bij elkaar op te tellen. Het idee is dat het mogelijk is het oneindig aantal afgeleiden op te tellen en tot één eindige som te komen.
In de wiskunde toont een Taylorreeks een functie als de som van een oneindige reeks. De termen van de som worden genomen uit de afgeleiden van de functie. Taylorreeksen komen voort uit de stelling van Taylor.
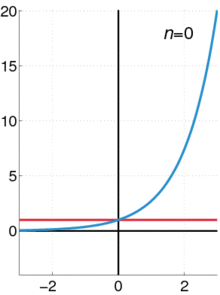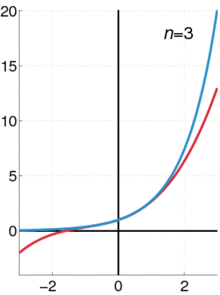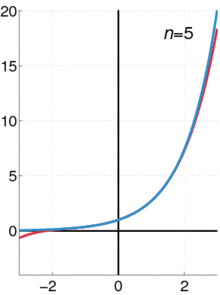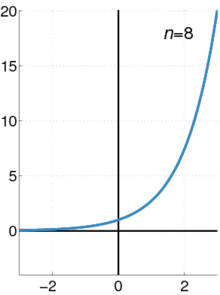
Een animatie die laat zien hoe een Taylorreeks kan worden gebruikt om een functie te benaderen. De blauwe lijn toont de exponentiële functie f ( x ) = e x {Displaystyle f(x)=e^{x}} 
Geschiedenis
De Oudgriekse filosoof Zeno van Elea kwam als eerste op het idee van deze reeks. De paradox genaamd "Zeno's parodox" is het resultaat. Hij geloofde dat het onmogelijk zou zijn om een oneindig aantal waarden op te tellen en als resultaat één eindige waarde te krijgen.
Een andere Griekse filosoof, Aristoteles, kwam met een antwoord op de filosofische vraag. Het was echter Archimedes die met een wiskundige oplossing kwam door gebruik te maken van zijn methode van uitputting. Hij kon bewijzen dat wanneer iets wordt opgesplitst in een oneindig aantal kleine stukjes, deze nog steeds één geheel vormen wanneer ze allemaal worden samengevoegd. De oude Chinese wiskundige Liu Hui bewees enkele honderden jaren later hetzelfde.
De vroegst bekende voorbeelden van de Taylorreeks zijn het werk van Mādhava van Sañgamāgrama in India in de jaren 1300. Latere Indiase wiskundigen schreven over zijn werk met de goniometrische functies van sinus, cosinus, tangens en arctangens. Geen van Mādhava's geschriften of verslagen bestaan vandaag de dag nog. Andere wiskundigen baseerden hun werk op Mādhava's ontdekkingen en werkten meer met deze reeksen tot de jaren 1500.
James Gregory, een Schotse wiskundige, werkte op dit gebied in de jaren 1600. Gregory bestudeerde de Taylor-reeks en publiceerde verschillende Maclaurin-reeksen. In 1715 ontdekte Brook Taylor een algemene methode om de reeks op alle functies toe te passen. (Al het eerdere onderzoek toonde hoe de methode alleen op specifieke functies kon worden toegepast). Colin Maclaurin publiceerde in de jaren 1700 een speciaal geval van de Taylor-reeks. Deze reeks, die rond nul is gebaseerd, wordt de Maclaurin reeks genoemd.
Definitie
Een Taylorreeks kan worden gebruikt om een functie ƒ(x) te beschrijven die een gladde functie is (of, in wiskundige termen, "oneindig differentieerbaar".) De functie ƒ kan reëel of complex zijn. De Taylorreeks wordt dan gebruikt om te beschrijven hoe de functie eruit ziet in de buurt van een getal a.
Deze Taylor-reeks, geschreven als een machtreeks, ziet er zo uit:
f ( a ) + f ′ ( a ) 1 ! ( x - a ) + f ″ ( a ) 2 ! ( x - a ) 2 + f ( 3 ) ( a ) 3 ! ( x - a ) 3 + ⋯ . {displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots . }
Deze formule kan ook in sigma notatie geschreven worden als:
∑ n = 0 ∞ f ( n ) ( a ) n ! ( x - a ) n {\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}},(x-a)^{n}}
Hierin is n! de factorie van n. ƒ (n)(a) is de n-de afgeleide van ƒ in het punt a. a {afgeleide a} 
Maclaurin serie
Wanneer a = 0 {\a6 a=0} 
f ( 0 ) + f ′ ( 0 ) 1 ! x + f ″ ( 0 ) 2 ! x 2 + f ( 3 ) ( 0 ) 3 ! x 3 + ⋯ . {\displaystyle f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots . }
Geschreven in sigma notatie, is de Maclaurin serie:
∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n {\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}},x^{n}}
Gemeenschappelijke Taylor-reeks
Enkele belangrijke Taylor-reeksen en Maclaurin-reeksen zijn de volgende.
sin x = ∑ n = 0 ∞ ( - 1 ) n ( 2 n + 1 ) ! x 2 n + 1 = x - x 3 3 ! + x 5 5 ! - ⋯ voor alle x {\displaystyle \sin x=sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\dots{ voor alle }}x}! }
cos x = ∑ n = 0 ∞ ( - 1 ) n ( 2 n ) ! x 2 n = 1 - x 2 2 ! + x 4 4 ! - ⋯ voor alle x {\displaystyle \cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}{2!}}+{\frac {x^{4}{4!}}-{\dots}{ voor alle }}x}! }
sinh ( x ) = ∑ n = 0 ∞ 1 ( 2 n + 1 ) ! x 2 n + 1 voor alle x {Displaystyle \sinh(x)=\sum _{n=0}^{infty }{frac {1}{(2n+1)!}}x^{2n+1}{text{ voor alle }}x}! }
cosh ( x ) = ∑ n = 0 ∞ 1 ( 2 n ) ! x 2 n voor alle x {Displaystyle \cosh(x)=sum _{n=0}^{infty }{frac {1}{(2n)!}}x^{2n}{text{voor alle }}x! }
e x = ∑ n = 0 ∞ 1 n ! x n = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + ⋯ voor alle x {\displaystyle e^{x}=sum _{n=0}^{\infty }{\frac {1}{n!}}x^{n}=1+x+{\frac {1}{2!}}x^{2}+{\frac {1}{3!}}x^{3}+{\dots}{ voor alle}x^{n! }
1 1 - x = ∑ n = 0 ∞ x n = 1 + x + x 2 + x 3 + x 4 + ⋯ voor alle | x | < 1 {\displaystyle {\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+x^{3}+x^{4}+\cdots {text{ voor alle }}|x|<1}
ln ( 1 + x ) = ∑ n = 1 ∞ ( - 1 ) n + 1 n x n voor alle | x | < 1 {\displaystyle \ln(1+x)=sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}x^{n}{text{voor alle }}|x|<1}
tan x = ∑ n = 1 ∞ B 2 n ( - 4 ) n ( 1 - 4 n ) ( 2 n ) ! x 2 n - 1 = x + x 3 3 + 2 x 5 15 + ⋯ voor | x | < π 2 {\displaystyle \tan x=sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots {text{ voor }}|x|<{\frac {\pi}{2}}}! }
Waarbij B n {\displaystyle B_{n}}

Vragen en antwoorden
V: Wat is een Taylorreeks?
A: Een Taylorreeks is een idee dat gebruikt wordt in computerwetenschappen, calculus, scheikunde, natuurkunde en andere soorten wiskunde op hoger niveau. Het is een reeks die gebruikt wordt om een schatting (gok) te maken van hoe een functie eruitziet.
V: Wat is het verschil tussen Taylorreeksen en Maclaurinreeksen?
A: Er is ook een speciale soort Taylorreeks die Maclaurinreeks heet.
V: Wat is de theorie achter de Taylorreeks?
A: De theorie achter de Taylorreeks is dat als er een punt op het coördinatenvlak (x- en y-as) gekozen wordt, het mogelijk is om te raden hoe een functie er in het gebied rond dat punt uit zal zien.
V: Hoe wordt de functie gecreëerd met behulp van Taylorreeksen?
A: Dit wordt gedaan door de afgeleiden van de functie te nemen en ze allemaal bij elkaar op te tellen. Het idee is dat het mogelijk is om het oneindige aantal afgeleiden op te tellen en te komen tot één eindige som.
V: Wat betekent een Taylorreeks in de wiskunde?
A: In de wiskunde toont een Taylorreeks een functie als de som van een oneindige reeks. De termen van de som worden genomen uit de afgeleiden van de functie.
V: Waar komen Taylorreeksen vandaan?
A: Taylorreeksen komen van de stelling van Taylor.
V: Op welke gebieden wordt de Taylorreeks vaak gebruikt?
A: De Taylorreeks wordt vaak gebruikt in computerwetenschappen, calculus, scheikunde, natuurkunde en andere soorten wiskunde op hoger niveau.
Zoek in de encyclopedie