Lagrangepunt
Lagrangepunten zijn stabiele posities in de buurt van grote lichamen in een baan om de aarde. Voorbeelden hiervan zijn twee grote objecten in een baan. Voorbeelden zijn te vinden in de banen van de Aarde en de Zon, of de Maan en de Aarde.
De punten zijn vijf plaatsen waar een klein voorwerp (zoals een door de mens gemaakte satelliet) in een baan kan draaien. Op die punten zijn de zwaartekrachten van de twee grote lichamen en de krachten door de beweging in evenwicht. Op die plaatsen houdt een klein voorwerp dus min of meer stabiel. In die punten bevinden zich stofwolken, asteroïden en door de mens gemaakte satellieten.
Dit effect is vernoemd naar de wiskundige Joseph-Louis Lagrange, die hierover in 1772 een artikel schreef (lang voordat we satellieten in een baan om de aarde brachten).
De vijf plaatsen worden L1, L2, L3, L4 en L5 genoemd. De eerste drie (L1, L2, L3) worden metastabiel genoemd, want als een satelliet een beetje uit de pas loopt, valt hij van dat punt af, en komt hij niet meer terug zonder brandstof te gebruiken. L4 en L5 worden als stabiel beschouwd - als een satelliet een beetje uit zijn plaats raakt zal hij door de zwaartekracht en de centripetale krachten weer op zijn plaats worden getrokken, en rond het Lagrangepunt oscilleren.
NASA heeft satellieten in twee Lagrangepunten van het zon-aardesysteem geplaatst. Het L1 punt (tussen de aarde en de zon) wordt gebruikt voor satellieten die naar de zon kijken, om te zoeken naar zonnevlammen. Het L2-punt (voorbij de aarde) wordt gebruikt voor ruimtetelescopen. Daar gaat de James Webb-ruimtetelescoop naartoe als hij gelanceerd wordt. Het is een miljoen mijl (1,6 miljoen kilometer) van de Aarde.
Omdat L4 en L5 stabiel zijn, hebben ze stofwolken aangetrokken, en minstens één asteroïde (voor het Earth-Sun-systeem - de grotere planeten hebben meer asteroïden in hun L4- en L5-punten). Deze asteroïden worden Trojaanse asteroïden genoemd.
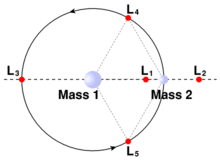
Lagrangepunten, voor 2 objecten
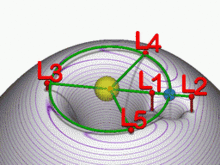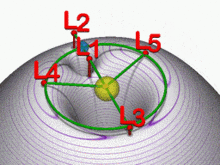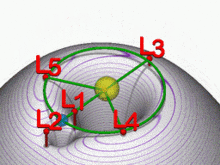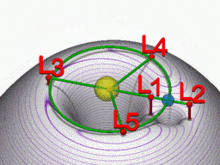
Lagrangiaanse punten met zwaartekrachtputten
Vragen en antwoorden
V: Wat zijn de punten van Lagrange?
A: Lagrangepunten zijn stabiele punten in de buurt van grote lichamen in een baan. Wanneer twee grote lichamen om elkaar heen draaien, zijn er plaatsen waar een derde lichaam zich kan vestigen, waardoor de gravitatie- en kinetische krachten van de twee grote lichamen in evenwicht komen, waardoor het kleine lichaam min of meer stabiel kan blijven.
V: Wie heeft het punt van Lagrange ontdekt?
Antwoord: Dit fenomeen is genoemd naar de wiskundige Joseph-Louis Lagrange, die er in 1772 een artikel over schreef (lang voordat satellieten in een baan om de aarde werden gebracht).
V: Hoeveel Lagrangepunten zijn er?
Antwoord: Er zijn vijf punten, genaamd L1, L2, L3, L4 en L5.
Vraag: Zijn alle Lagrangepunten stabiel?
A: De eerste drie (L1, L2, L3) worden metastabiel genoemd, want als een satelliet iets uit positie raakt, zal hij van dat punt wegvallen en niet meer terugkomen zonder brandstof te gebruiken. L4 en L5 worden daarentegen als stabiel beschouwd - als de satelliet iets uit positie raakt, zullen de zwaartekracht en de middelpuntvliedende kracht hem weer op zijn plaats trekken.
V: Wat voor banen gebruiken de satellieten op deze posities?
Antwoord: Op deze locaties kunnen satellieten halo-banen gebruiken om de zon te observeren op zoek naar zonnevlammen, of ze kunnen worden gebruikt voor ruimtetelescopen zoals de James Webb Space Telescope, die op 25 december 2021 wordt gelanceerd en zich op ongeveer een miljoen mijl (ongeveer 1,5 miljoen kilometer) van de aarde zal bevinden.
V. Welke voorwerpen zijn van nature aanwezig op deze plaatsen?
Antwoord: Omdat L4 en L5 stabiel zijn, hebben zij stofwolken en asteroïden aangetrokken, de zogenaamde Trojaanse asteroïden, die grotere planeten vaker bevolken dan kleinere planeten, zoals het Aarde-Zon-systeem, dat weinig asteroïden heeft aangetrokken.
Zoek in de encyclopedie