Onzekerheidsrelatie van Heisenberg | ook wel het Heisenberg onzekerheidsprincipe genoemd

Diagrammen

 
6. Deze animatie toont een van de belangrijke gevolgen van de onzekerheid van het universum: kwantumtunneling van elektronen. Kijk goed. Telkens komt er een beetje door de barrière heen.  


5. Door de opening in het midden op te hangen met behulp van veerschalen kan het momentum worden gemeten, maar door dit te doen beweegt de opening onvoorspelbaar, zodat informatie over de locatie van elk foton in het midden verloren gaat.  


4. Als een barrière met een klein gaatje wordt voorzien van een veer, knijpt het deeltje door het gaatje, waardoor de barrière wordt ingedrukt, de veren worden uitgerekt en zo het momentum wordt gemeten. Maar omdat de verende barrière beweegt, weten we minder zeker waar het deeltje zich bevond toen het door het gat ging, en ook diffractie zal de positie op het detectiescherm beïnvloeden.  


3. Door het gat te vernauwen wordt de zekerheid van de plaats waar het foton zich in het midden bevindt vergroot, maar de richting van daar naar het detectiescherm rechts wordt navenant onzekerder. De focus wordt vaag. Door het gat wijder te maken komen de fotonen allemaal in het midden van het detectiescherm terecht, maar dan hebben we minder een idee van waar ze waren toen ze door de centrale barrière gingen.  


1. Fotonen, elektronen en andere subatomaire deeltjes komen scherp in beeld als ze door een groot gat worden geschoten, maar we weten niet precies waar ze zich in het midden van hun pad bevonden.  


2. Door het gat te vernauwen worden de paden van de deeltjes rond de randen van het gat afgebogen (diffractie), zodat de resulterende bundel groter en zachter wordt.  

Hoe heeft de mens onzekerheid leren kennen?

Zeer kort nadat Werner Heisenberg de nieuwe kwantumfysica had gecreëerd kwam er iets onverwachts uit zijn wiskunde, de uitdrukking:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x,\Delta p \frac {h}{4pi }}\qquad \qquad }

Het bereik van de fout in positie (x) maal het bereik van de fout in impuls (p) is ongeveer gelijk aan of groter dan de constante van Planck gedeeld door 4π.

Deze symbolen verwoorden in wiskundige vorm wat u al in de bovenstaande afbeeldingen hebt gezien. De symbolen zeggen op een duidelijke manier dat u niet volkomen zeker kunt zijn van waar iets is en waar het naartoe gaat. Als u duidelijker weet waar het zich op een bepaald moment bevindt, hebt u minder een idee over waar het naartoe gaat en hoe snel. Als u duidelijker wordt over waar het op enig moment naartoe gaat en hoe snel, dan hebt u minder een idee van waar het nu is.

Wetenschappers hadden al geleerd waarom bepaalde stoffen karakteristieke kleuren licht afgeven wanneer ze worden verhit of anderszins opgewonden. Heisenberg probeerde uit te leggen waarom deze kleuren elk een karakteristieke helderheid hebben. Het zou niet goed genoeg zijn geweest als hij en de andere wetenschappers gewoon hadden gezegd: "Nou, zo is het nu eenmaal." Zij waren er zeker van dat er een goede reden moest zijn voor deze verschillen, en voor het feit dat de verhoudingen tussen de helderheidslijnen altijd hetzelfde waren voor elk monster van een element.

Hij had geen idee dat hij zou struikelen over een verborgen geheim van de natuur toen hij op zoek ging naar de verklaring voor de intensiteit van de gekleurde lijnen die kenmerkend zijn voor elk van de elementen. De studie van de kwantummechanica had al aangetoond waarom waterstof vier heldere lijnen heeft in het deel van het spectrum dat de mens kan zien. Het moet hebben geleken dat het volgende dat moest worden geleerd gewoon zou zijn hoe hun helderheid te berekenen. Waterstof leek de voor de hand liggende plaats om te beginnen, omdat waterstof slechts één elektron heeft, en slechts vier lijnen in het zichtbare deel van het spectrum. Er moet toch een goede reden zijn waarom ze niet even helder zijn. De verklaring voor de helderheid van de verschillend gekleurde lijnen van neon en de andere elementen kon wachten.

Heisenberg begon te werken aan kwantumfysica door de klassieke vergelijkingen voor elektriciteit aan te passen, die om te beginnen erg ingewikkeld zijn, dus de wiskunde achter zijn paper uit 1925 was erg moeilijk te volgen.

Hij probeerde de juiste manier te vinden om de intensiteit van heldere lijnen in het spectrum van de waterstoflamp te berekenen. Hij moest een verwante grootheid vinden die "amplitude" werd genoemd en die met amplitude vermenigvuldigen (of met andere woorden, hij moest de amplitude kwadrateren) om de gewenste intensiteit te krijgen. Hij moest uitzoeken hoe de amplitude uit te drukken op een manier die rekening hield met het feit dat waterstoflampen niet bij alle frequenties stralen, en niet uitstralen over een continu bereik van frequenties in het deel van het spectrum dat mensen kunnen zien. Heisenberg vond een opmerkelijke nieuwe manier om de amplitude te berekenen.

De vreemde vergelijking die Heisenberg ontdekte en gebruikte om de vermenigvuldiging van een kwantumgrootheid (bijv. positie) met een andere (bijv. momentum) te doen, werd gepubliceerd in wat wel "Heisenberg's 'magische' paper van juli 1925" werd genoemd.

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {C(n,n-b)=sum _{a}^{},A(n,n-a)B(n-a,n-b)}.

De bovenstaande wiskunde ziet er erg moeilijk uit, maar de wiskunde die eraan voorafgaat is nog veel moeilijker en uiterst moeilijk te begrijpen. Het is hier alleen gegeven om te laten zien hoe het eruit zag. Het document van Heisenberg is een historische mijlpaal. Veel van de natuurkundigen die zijn paper lazen zeiden dat zij het niet oneens konden zijn met zijn conclusies, maar dat zij zijn uitleg over hoe hij tot die conclusies was gekomen niet konden volgen. De beginvergelijkingen die Heisenberg gebruikte, hadden betrekking op Fourier-reeksen, en omvatten vele factoren. We komen nog terug op de bovenstaande vergelijking, omdat het een soort recept is voor het uitschrijven en vermenigvuldigen van matrices.

De nieuwe vergelijkingen moesten zo vreemd en ongewoon zijn omdat Heisenberg een vreemde wereld beschreef waarin sommige dingen, zoals de banen van elektronen, niet langzaam groter of kleiner worden. De nieuwe soorten veranderingen gaan gepaard met sprongen en grote gaten tussen sprongen. Elektronen kunnen alleen springen tussen bepaalde banen, en de energie die wordt gewonnen of verloren bij het wisselen tussen banen wordt geproduceerd wanneer een foton van de juiste energie wordt geabsorbeerd of een nieuw foton van de juiste energie wordt geproduceerd. Als elektronen in waterstofatomen het vaakst naar beneden springen (vallen) tussen twee bepaalde banen, dan zullen er meer fotonen worden uitgezonden op dat energieniveau, en dus zal het licht dat op dat niveau wordt geproduceerd het meest intens zijn.

Het was moeilijk om vergelijkingen voor continue spectra (wat je ziet als je het licht van de zon door een prisma haalt) geschikt te maken voor spectra met slechts een paar piekfrequenties waartussen niets zit. Bijna alles wat men al had geleerd over licht en energie was gedaan met grote dingen zoals brandende kaarsen of zonnen, en die grote objecten produceren allemaal continue spectra. Ook al waren deze gewone dingen gemakkelijk om experimenten mee te doen, toch had het veel tijd gekost om de (natuurkundige) wetten die daarop van toepassing zijn te achterhalen. Nu hadden natuurkundigen te maken met dingen die te klein waren om te zien, dingen die geen continue spectra produceerden, en probeerden zij een manier te vinden om tenminste aanwijzingen te krijgen van wat zij al wisten die hen zouden helpen de wetten van deze kleine en afgesloten lichtbronnen te vinden.

De oorspronkelijke vergelijkingen hadden betrekking op een soort vibrerend lichaam dat een golf zou produceren, een beetje zoals een riet in een orgel een geluidsgolf met een karakteristieke frequentie zou produceren. Er was dus beweging heen en weer (zoals het trillen van een riet) en er was een uitgezonden golf die kon worden weergegeven als een sinusgolf. Veel van wat eerder was uitgevonden over natuurkunde op atomair niveau had te maken met elektronen die rond kernen bewegen. Wanneer een massa in een baan beweegt, wanneer zij rond een soort middelpunt draait, heeft zij een zogenaamd "impulsmoment". Hoekmomentum is de manier waarop iets als een draaimolen blijft draaien nadat men is gestopt met duwen. De wiskunde voor faseberekeningen en impulsmoment is ingewikkeld. Bovendien liet Heisenberg niet al zijn berekeningen zien in zijn artikel uit 1925, dus zelfs goede wiskundigen kunnen moeite hebben met het invullen van wat hij niet zei.

Hoewel veel natuurkundigen zeiden dat zij de verschillende wiskundige stappen in Heisenbergs doorbraakdocument niet konden achterhalen, gebruikt een recent artikel dat probeert uit te leggen hoe Heisenberg aan zijn resultaat kwam, twintig pagina's vol met wiskunde. Zelfs dat artikel is niet gemakkelijk te begrijpen. De wiskunde begon met heel moeilijke dingen en leverde uiteindelijk iets relatief eenvoudigs op dat bovenaan dit artikel wordt getoond. Het eenvoudiger resultaat bereiken was niet eenvoudig, en we gaan niet proberen het proces te laten zien om van een verouderd beeld van het universum tot de nieuwe kwantumfysica te komen. We hebben net genoeg details nodig om te laten zien dat vrijwel direct na de doorbraak van Heisenberg een deel van de werking van het universum in beeld kwam dat niemand ooit eerder had gezien.

Heisenberg moet erg opgewonden maar ook erg moe zijn geweest toen hij 's avonds laat eindelijk zijn doorbraak maakte en voor zichzelf begon te bewijzen dat het zou werken. Vrijwel meteen merkte hij iets vreemds op, iets waarvan hij dacht dat het een vervelend probleempje was dat hij op de een of andere manier kon laten verdwijnen. Maar het bleek dat dit kleine ongemak een grote ontdekking was.

Heisenberg had gewerkt aan het vermenigvuldigen van amplitudes met amplitudes, en nu had Heisenberg een goede manier om amplitude uit te drukken met behulp van zijn nieuwe vergelijking. Natuurlijk dacht hij na over vermenigvuldiging, en over hoe hij dingen zou vermenigvuldigen die werden gegeven in termen van ingewikkelde vergelijkingen.

Heisenberg realiseerde zich dat naast squaring amplitude hij uiteindelijk zou willen vermenigvuldigen positie door momentum, of vermenigvuldigen energie door tijd, en het leek alsof het zou een verschil maken als hij draaide de volgorde in deze nieuwe gevallen. Heisenberg vond niet dat het uit moest maken of men positie met momentum vermenigvuldigde of dat men momentum met positie vermenigvuldigde. Als het gewoon simpele getallen waren geweest, zou er geen probleem zijn geweest. Maar het waren allebei ingewikkelde vergelijkingen, en hoe je de getallen in de vergelijkingen moest stoppen bleek verschillend te zijn, afhankelijk van de manier waarop je begon. In de natuur moest je de positie meten en dan het momentum, of anders moest je het momentum meten en dan de positie, en in de wiskunde gold dezelfde algemene situatie. (Zie het Engelse Wikipedia-artikel Heisenberg's entryway to matrix mechanics als u de pietluttige details wilt leren kennen). De kleine maar vervelende verschillen tussen de resultaten zouden blijven bestaan, hoezeer Heisenberg ook wenste dat ze zouden verdwijnen.

Op dat moment kon Heisenberg zich niet ontdoen van dat ene probleempje, maar hij was uitgeput, dus leverde hij zijn werk in bij zijn directe supervisor, Max Born, en ging op vakantie.

Max Born was een opmerkelijk wiskundige die al snel zag dat de vergelijking die Heisenberg hem had gegeven een soort recept was voor het schrijven van een matrix. Dr. Born was in die tijd een van de weinige mensen die geïnteresseerd was in dit vreemde soort wiskunde waarvan de meeste mensen dachten dat het niet veel voorstelde. Hij wist dat matrices konden worden vermenigvuldigd, zodat alle berekeningen voor de boekhouding van een natuurkundig probleem konden worden uitgevoerd door de ene matrix met de andere te vermenigvuldigen. Als je een ingewikkelde procedure in een standaard en aanvaardbare vorm kon gieten, zou het gemakkelijker zijn om ermee te werken. Het zou het ook gemakkelijker maken voor andere mensen om het te accepteren.

Born was zo'n goede wiskundige dat hij vrijwel onmiddellijk besefte dat het omwisselen van de volgorde van vermenigvuldiging van de twee matrices een ander resultaat zou opleveren, en de resultaten zouden een klein beetje verschillen. Dat verschil zou h/2πi zijn. In het dagelijks leven zou dat verschil zo klein zijn dat we het niet eens zouden kunnen zien.

 
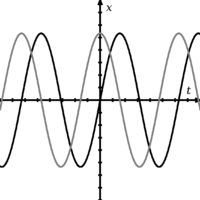
Twee golven die uit fase zijn met elkaar  


Waterstofspectrum  


Neon spectrum  


Volledig visueel spectrum van de zon. Er zijn geen hiaten. Deze grafiek toont de intensiteiten bij de verschillende frequenties.  


Wanneer bepaalde moleculen worden aangeslagen, geven ze een karakteristieke kleur af.  

Op naar een formele theorie van onzekerheid

Het duurde een paar jaar, maar Heisenberg was in staat om het Onzekerheidsprincipe te bewijzen, dat zegt dat Δx × Δp = h/2, wat het getal is dat uit de oorspronkelijke vergelijkingen komt, maar de π en de i die te maken hebben met faseveranderingen weglaat. Heisenberg verklaarde dat hij zijn onzekerheidsprincipe afleidde uit dit eerdere resultaat toen hij in 1927 een artikel schreef waarin hij deze theorie introduceerde.

De constante geschreven h, genaamd de constante van Planck, is een mysterieus getal dat vaak voorkomt, dus we moeten begrijpen wat dit kleine getal is. Numeriek wordt het meestal gegeven als 6,62607×10^-34 J s (joule-seconden). Het is dus een grootheid waarbij energie en tijd een rol spelen.

Het werd ontdekt toen Planck zich realiseerde dat de energie van een perfecte straler (een zwart lichaam straler genoemd) wordt uitgezonden in eenheden van bepaalde grootte die "quanta" worden genoemd (het enkelvoud van dit woord is "quantum"). Uitgestraalde energie wordt uitgezonden als fotonen, en de frequentie van een foton is evenredig met de "stoot" die het afgeeft. Wij ervaren verschillende frequenties van zichtbaar licht als verschillende kleuren. Aan het violette uiteinde van het spectrum heeft elk foton een relatief grote hoeveelheid energie; aan het rode uiteinde van het spectrum heeft elk foton een relatief kleine hoeveelheid energie. De manier om de hoeveelheid energie van een foton te berekenen wordt gegeven door de vergelijking E = hν (energie is gelijk aan de constante van Planck maal "nu" of frequentie).

Het Heisenberg onzekerheidsprincipe Δx × Δp ≥ h vertelt ons dat wanneer we proberen bepaalde getallenparen vast te stellen, we er maar zo dicht bij kunnen komen, en dat als we proberen een van de getallen duidelijker te krijgen, d.w.z. als we proberen Δx kleiner te maken zodat we een beter idee krijgen van de positie van iets, we een groter getal terug moeten krijgen voor het andere getal van het paar, en dat de hoeveelheid waarmee de twee verschillen nauw samenhangt met h.

Een ander paar natuurkundige grootheden gaat volgens de onzekerheidsrelatie: ΔE × Δt ≥ h, en dat paar geeft onder andere aan dat als we in de interstellaire ruimte kijken, een plek waar we helemaal niets zouden verwachten aan te treffen, en we Δt steeds dichter bij 0 brengen, dat dan om het evenwicht in de vergelijking te bewaren ΔE steeds groter moet worden - en plotseling kan er iets met momentum ontstaan, alleen maar voor die korte periode.

Hoe is deze onbepaaldheid (gebrek aan zekerheid) te verklaren? Wat gebeurt er in het heelal? Er wordt vaak gezegd dat een nieuwe theorie die succesvol is, nieuwe informatie kan opleveren over de onderzochte verschijnselen. Heisenberg creëerde een wiskundig model dat de juiste intensiteiten voorspelde voor het helderstroomspectrum van waterstof, maar zonder dat hij dit van plan was ontdekte hij dat bepaalde paren van fysische grootheden een onverwachte onzekerheid onthullen. Tot op dat moment had niemand enig idee dat metingen niet eeuwig preciezer en nauwkeuriger konden worden gemaakt. Het feit dat ze niet zekerder, vaster konden worden gemaakt, was een verbluffende nieuwe ontdekking. Veel mensen waren niet bereid dit te accepteren.

Bohr en zijn collega's betoogden dat fotonen, elektronen, enz. geen positie of impuls hebben totdat zij worden gemeten. Dit theoretische standpunt kwam voort uit de ontdekking van onzekerheid, en was niet zomaar een persoonlijke voorkeur voor wat men moest geloven. Bohr zei dat wij niets weten over iets als een foton of elektron totdat wij het waarnemen. Om zo'n klein ding waar te nemen moeten wij er op de een of andere manier mee in wisselwerking staan. In het dagelijks leven is het mogelijk om bijvoorbeeld naast een auto te lopen en te noteren wanneer deze punten op een rooster op het trottoir kruist. Misschien drukt het gewicht van de auto zelf op kleine hendels in het trottoir die de aan elk ervan bevestigde klokken uitzetten en het gewicht van de auto registreren. Uiteindelijk zouden we een duidelijk overzicht hebben van waar de auto zich op verschillende tijdstippen bevond, en zouden we ook de voortgangsrichting en het gewicht kunnen berekenen. We zouden dan op elk moment van de klok zowel zijn positie als zijn momentum (zijn snelheid vermenigvuldigd met zijn massa) kunnen weten. We zouden ons zelfs niet kunnen voorstellen dat de kracht die nodig is om de kleine hendels te bewegen enige invloed zou hebben op de voortgang van de auto. Wij zouden ons ook niet kunnen voorstellen dat de auto geen plaats of traject heeft tussen de punten op het trottoir waar zich hendels bevinden, of dat de auto gedurende die tijd in een soort driedimensionale waas bestaat en alleen tot rust komt als hij een hendel indrukt. De wereld waarmee wij vertrouwd zijn laat dit soort vreemde interacties niet zien.

Om een schip op zee tijdens de donkerste nacht te lokaliseren zouden wij een zoeklicht kunnen gebruiken, en dat licht zou de positie of de reisrichting van het schip niet verstoren, maar om een elektron met licht te lokaliseren zou het met één of meer fotonen moeten worden geraakt die elk genoeg impuls hebben om de positie en de baan van het elektron te verstoren. Om het elektron met andere middelen te lokaliseren zou het in een soort fysieke beperking moeten worden gehouden die ook zijn voorwaartse beweging zou beëindigen.

Om een foton te lokaliseren, kan men het best door een cirkelvormig gat in een barrière laten gaan, zonder zijn voorwaartse beweging te beëindigen. Als men het tijdstip kent waarop het foton werd uitgezonden (bijvoorbeeld door een laser) en het tijdstip waarop het foton aankomt bij een detectiescherm zoals een digitale camera, dan kan men de tijd berekenen die nodig is om die afstand af te leggen en het tijdstip waarop het foton door het gat ging. Om het foton te laten passeren, moet het cirkelvormige gat echter een diameter hebben die groter is dan de grootte van het foton. Hoe kleiner het cirkelvormige gat wordt gemaakt, hoe dichter we bij de exacte positie van het foton komen als het erdoorheen gaat. We kunnen echter nooit weten of het foton op dat moment uit het midden is. Als het gat precies even groot is als het foton, gaat het er niet doorheen. Naarmate de diameter van het gat kleiner wordt, verandert het momentum of de richting van het foton bij het verlaten van het gat steeds sterker.

Niels Bohr en zijn collega's stelden dat we in grote problemen komen als we van de dingen die te klein zijn om zelfs met een microscoop te zien, alles voor waar aannemen waarvoor we alleen bewijs hebben op de schaal van het dagelijks leven. In het dagelijks leven hebben de dingen altijd een vaste positie. Op atomaire schaal hebben we geen bewijs voor die conclusie. In het dagelijks leven hebben dingen een bepaalde tijd waarop ze zich voordoen. Op de atomaire schaal hebben we geen bewijs om die conclusie te ondersteunen. Als men in het dagelijks leven een fabriek observeert vanaf de nachtploeg van dag één tot de dagploeg van dag twee en men ziet een afgewerkte auto naar het laadperron rollen, dan heeft het geen zin om te zeggen dat het onmogelijk is om te zeggen of hij tijdens de nachtploeg of tijdens de dagploeg is afgeleverd. Maar op atomaire schaal kunnen we gevallen laten zien waarin we een enkel foton moeten tellen als geproduceerd op twee tijdstippen. (Als dat nog niet erg genoeg is, kunnen we ook gevallen laten zien waarin een enkel foton wordt geproduceerd door twee naast elkaar gelegen lasers).

Een deel van de moeilijkheid bij het achterhalen van wat er op atomaire schaal gebeurt, is dat wij zowel willen weten waar iets is als wat zijn baan is, en dat wij beide dingen tegelijk willen weten, maar wij kunnen positie en baan niet tegelijk meten. Wij meten ofwel het momentum van een foton of elektron op één moment en meten dan zonder meer dan nodig de positie ervan, of wij draaien de zaken om en meten eerst de positie en daarna het momentum. Het probleem is dat door de eerste een vrij definitieve vorm aan te nemen (door er op de een of andere manier op te drukken) wij de onzekerheid verhogen die betrokken is bij de volgende meting. Als onze eerste metingen zo grof waren dat er bij elke meting veel fout werd geïntroduceerd, dan zouden we de zaken kunnen verbeteren door ze telkens lichter aan te pakken, maar we zouden nooit verder kunnen komen dan een bepaalde nauwkeurigheidsgrens.

Wij weten uit het dagelijks leven dat een poging om iets te wegen op een badkamerweegschaal die op een wasmachine in het centrifugeprogramma staat, onnauwkeurige resultaten oplevert omdat de naald op de weegschaal erg schommelt. We kunnen de wasmachine uitzetten. Maar voor zeer nauwkeurige metingen merken we dat voorbijrijdende vrachtwagens in de buurt de naald doen trillen, dus kunnen we de weegschaal op iets zetten om hem te isoleren van de storingen van buitenaf. Wij denken dat wij de trillingen voldoende kunnen elimineren om de resultaten zo nauwkeurig te krijgen als wij willen. Wij denken er nooit aan dat het ding op de weegschaal zelf trilt of dat het een onbepaald momentum bezit.

Terugredenerend vanuit het Onzekerheidsprincipe lijkt het erop dat er in feite geen vaststaande positie en geen vaststaand momentum bestaat voor enig ding op atomaire schaal, en dat experimentators de dingen alleen tot vaststaandheid kunnen dwingen binnen de grenzen van het Onzekerheidsprincipe. Bohr en zijn collega's betoogden alleen dat wij niets konden weten zonder metingen te doen, en wanneer de metingen werden gedaan, kunnen wij dingen in de richting van definitievere positie of definitiever momentum duwen, maar dat wij niet de absolute definitiefheden of de zekerheid kunnen krijgen die wij zouden willen. Maar anderen namen de mogelijkheid serieus, en betoogden dat als de wiskunde klopt, er geen zekerheid kan zijn in de wereld van het ultrakleine. De aard van de wetenschap is dat de wiskunde slechts een model van de werkelijkheid is, en er is geen garantie dat het een correct model is.

De wiskunde en de praktische gevolgen van de dingen die de wiskunde voorspelt zijn zo betrouwbaar dat ze moeilijk te weerleggen zijn, maar wat de wiskunde zegt over de echte wereld heeft verschillende ideeën opgeleverd. Onder de wetenschappers die met Niels Bohr in Kopenhagen werkten, werd het onzekerheidsprincipe opgevat als dat het fysieke universum op een elementair niveau niet bestaat in een deterministische vorm. Het is veeleer een verzameling waarschijnlijkheden of potentialen.

Tegenover het verhaal dat door de Kopenhagen-groep rond de wiskunde is geweven, staan andere verhalen, zoals de "meervoudige universum-interpretatie", die stelt dat telkens wanneer er volgens de kwantumtheorie meerdere mogelijke uitkomsten zijn, elke uitkomst zich voordoet in een eigen nieuw universum. Einstein stelde dat er geen meervoudige mogelijke uitkomsten zijn, dus is er maar één universum en dat is gedetermineerd, of, zoals hij het uitdrukte: "God dobbelt niet."

 
Als h de kleinst mogelijke hoeveelheid energie zou zijn, dan zou de basisvergelijking die de energie in fotonen van verschillende frequentie weergeeft, niet in evenwicht zijn. Dat zou fout zijn.  

Bezwaren tegen het onzekerheidsprincipe

Albert Einstein zag dat de nieuwe kwantummechanica een gebrek aan positie en momentum impliceerde in de tijd voorafgaand aan de metingen, en hij maakte daartegen ernstig bezwaar. Hij was er vast van overtuigd dat de dingen bepaalde posities en bepaalde impulsen hadden voordat ze werden gemeten, en dat het feit dat het meten van een van een paar dingen de mogelijkheid om het andere nauwkeurig te meten verstoort, niet bewijst dat een van beide vooraf ontbreekt. Hij en twee van zijn collega's schreven wat bekend is geworden als het "EPR-paper". Dat artikel stelt dat er eigenschappen moeten zijn die positie en impuls bepalen, en dat als we die zouden kunnen zien, of als we er informatie over zouden kunnen krijgen, we positie en impuls wiskundig zouden kunnen kennen en voorspellen. Lange tijd dacht men dat er geen manier was om te bewijzen of te weerleggen wat voor Einstein een geloofsartikel was. Het argument was zeer productief, want het leidde tot alle moderne ontwikkelingen op het gebied van verstrengeling.

Wiskundig gezien heeft Einstein ongelijk gekregen. In 1964 ontwikkelde John Stewart Bell een wiskundige methode om onderscheid te maken tussen het gedrag van twee deeltjes die bepaalde toestanden hebben die slechts onbekend zijn voor de twee personen die ze onderzoeken, en twee deeltjes die verstrengelde toestanden hebben die onbepaald of onzeker zijn totdat ze worden gemeten. Zijn methode toont aan dat de waarschijnlijkheid van bepaalde resultaten verschillend is onder de twee verschillende aannames. Zijn werk wordt de stelling van Bell of de ongelijkheid van Bell genoemd. Experimenten hebben aangetoond dat de natuur zich gedraagt zoals Bell beschrijft.

 

Een andere weg naar onzekerheid

De eerste discussies over het onzekerheidsprincipe van Heisenberg berustten op een model dat er geen rekening mee hield dat materiedeeltjes zoals elektronen, protonen, enz. een golflengte hebben. In 1926 toonde Louis de Broglie aan dat alle dingen, niet alleen fotonen, hun eigen frequentie hebben. Dingen hebben een golfkarakter en een deeltjeskarakter, net als fotonen. Als we proberen de golf van een ding als een proton smaller en langer te maken, zou dat zijn positie duidelijker maken, maar dan zou het momentum minder goed gedefinieerd worden. Als wij proberen het impulsmoment deel van een golfbeschrijving duidelijker te maken, d.w.z. het binnen een kleiner bereik van waarden te houden, dan spreidt de golfpiek zich uit en wordt zijn positie minder duidelijk.

De golf die deel uitmaakt van de beschrijving van een foton is in de kwantummechanica niet hetzelfde soort ding als een golf op het oppervlak van de oceaan of de gebieden van samengeperste lucht en ijle lucht waaruit geluidsgolven bestaan. In plaats daarvan hebben deze golven pieken of gebieden met een hoge amplitude die te maken hebben met de waarschijnlijkheid dat er op dat punt in ruimte en tijd iets te vinden is. Om precies te zijn is het het kwadraat van de amplitude dat de waarschijnlijkheid aangeeft dat een bepaald verschijnsel zich voordoet.

De golf die van toepassing is op een foton kan een zuivere sinusgolf zijn. In dat geval geeft het kwadraat van de waarde van elke piek de kans om het foton op dat punt waar te nemen. Aangezien de amplitudes van de sinusgolven overal hetzelfde zijn, zou de kans om het foton op elk van die punten te vinden hetzelfde zijn. Praktisch gesproken zou het kennen van de golf voor een van deze fotonen dus geen aanwijzing geven over waar het foton gezocht moet worden. Anderzijds is het momentum van een foton wiskundig gerelateerd aan de amplitude van zijn golf. Aangezien we in dit geval een zuivere sinusgolf hebben, is de amplitude van elke cyclus van de golf hetzelfde en daarom is er slechts één impulswaarde verbonden aan deze golf. We zouden niet weten waar het foton zou inslaan, maar we zouden wel precies weten hoe hard het zou inslaan.

In lichtbundels die gericht zijn op een bepaald punt op een detectiescherm, zijn de golven die gepaard gaan met de fotonen geen zuivere sinusgolven. In plaats daarvan zijn het golven met een hoge amplitude op één punt en veel lagere amplitudes aan weerszijden van die hoogste piek. Wiskundig is het mogelijk een dergelijke golf te analyseren in een aantal verschillende sinusgolven van verschillende golflengte. Het is iets gemakkelijker om het omgekeerde van dit proces te visualiseren door te kijken naar een initiële sinusgolf van één frequentie waaraan een tweede sinusgolf van een andere golflengte wordt toegevoegd, dan een derde, dan een vierde, enzovoort. Het resultaat zal een complexe golf zijn die één hoge piek vertoont en een groot aantal golven van verschillende golflengte en dus van verschillende momentum bevat. In dat geval is de kans dat het foton op een bepaald punt verschijnt extreem groot, maar het momentum dat het levert kan gerelateerd blijken te zijn aan de golflengte van een van de samenstellende golven. Met andere woorden, de waarde van p = ħ/λ is niet langer één waarde, omdat alle lengtes van de samengestelde "golven met verschillende golflengte" in aanmerking moeten worden genomen.

De simulatie laat zien hoe de verscherping van de locatie van een deeltje wiskundig kan worden gemodelleerd: Plaats veel verschillende golfvormen over de oorspronkelijke sinusgolf. Het centrum zal een steeds hogere piek vormen, en de rest van de pieken zal in aantal toenemen maar in hoogte afnemen omdat ze met elkaar interfereren. Dus uiteindelijk zijn er veel verschillende golven in de superpositie, elk met een andere golflengte en (door p = ħ/λ) een ander momentum, maar slechts één zeer hoge piek, één die steeds hoger en smaller wordt en ons iets geeft dat steeds dichter bij een bepaalde positie komt.

Om het momentum steeds duidelijker te maken, zouden we steeds meer van de boven elkaar liggende sinusgolven moeten weghalen totdat we alleen nog een eenvoudige sinusgolf overhouden. Daarbij zouden we de hoogte van de centrale piek geleidelijk verminderen en de hoogtes van de concurrerende plaatsen waar het deeltje zich zou kunnen bevinden geleidelijk verhogen.

Dus wanneer we beginnen met een golfbeeld van subatomaire deeltjes, zullen we typisch altijd te maken hebben met gevallen met relatief hoge centrale pieken en relatief veel componentgolflengten. Er zal nooit een exacte positie of een exact momentum worden voorspeld onder deze omstandigheden. Als het wiskundige model een nauwkeurige weergave is van de werkelijke wereld, dan heeft geen enkel foton of ander subatomair deeltje een exacte positie of een bepaald momentum. Wanneer we zo'n deeltje meten, kunnen we een methode kiezen die de piek verder afknijpt en smaller maakt, of we kunnen een methode kiezen die de piek verlaagt en de golflengten van de componenten gelijk maakt. Afhankelijk van wat we meten en hoe we het meten, kunnen we onze locatie duidelijker laten uitkomen of kunnen we ons impulsbereik smaller maken. We kunnen er bij het ontwerp van het experiment op letten dat we de apparatuur niet op verschillende manieren kunnen manipuleren, maar we kunnen ons niet ontdoen van het feit dat er aanvankelijk niets helemaal zeker was.

 
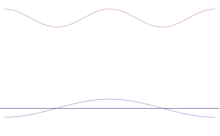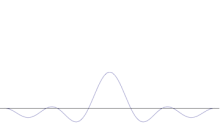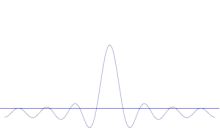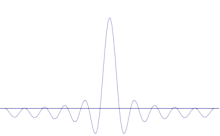
De superpositie van verschillende vlakke golven. Het golfpakket wordt steeds lokaler naarmate er meer golven bijkomen. De Fouriertransformatie is een wiskundige bewerking die een golfpakket scheidt in zijn afzonderlijke vlakke golven. Merk op dat de hier getoonde golven alleen ter illustratie reëel zijn, terwijl in de kwantummechanica de golffunctie over het algemeen complex is.  

Culturele invloeden

Het onzekerheidsprincipe van Heisenberg heeft de argumenten over de vrije wil sterk beïnvloed. Volgens de theorieën van de klassieke natuurkunde is het mogelijk te stellen dat de wetten van oorzaak en gevolg onverbiddelijk zijn en dat als het universum eenmaal op een bepaalde manier is begonnen, de interacties van alle materie en energie die in de toekomst zullen plaatsvinden, kunnen worden berekend vanuit die begintoestand. Aangezien alles absoluut het resultaat is van wat eraan voorafging, zo stelden zij, is elke beslissing die een mens neemt en elke situatie waarin die mens terechtkomt al vanaf het begin der tijden voorbestemd. We hebben dan geen keuze in wat we doen.

Mensen die in de vrije wil geloven, stellen dat de wetten van de kwantummechanica niet voorspellen wat er zal gebeuren, maar alleen wat meer en minder waarschijnlijk is. Daarom is elke actie het resultaat van een reeks willekeurige "muntopgooien" en kan geen enkele beslissing worden herleid tot een reeks noodzakelijke voorwaarden.

De uitdrukkingen "kwantumsprong" en "quantumsprong" zijn gewone manieren geworden om over dingen te praten. Meestal bedoelt men iets te beschrijven als een enorme verandering die in korte tijd plaatsvindt. De term is eigenlijk van toepassing op de manier waarop een elektron zich gedraagt in een atoom, hetzij wanneer het een foton van buitenaf absorbeert en zo van een baan rond de atoomkern naar een hogere baan springt, hetzij wanneer het een foton uitzendt en zo van een hogere baan naar een lagere baan valt. Het idee van Niels Bohr en zijn collega's was dat het elektron niet beweegt tussen banen, maar dat het uit de ene baan verdwijnt en onmiddellijk in een andere baan verschijnt. Een kwantumsprong is dus eigenlijk geen wereldschokkende verandering, maar een plotselinge kleine verandering.

Wanneer de mens één of ander proces op subatomaire schaal meet en het onzekerheidsprincipe manifesteert zich, dan kan men zeggen dat de menselijke actie het ding beïnvloed heeft dat werd gemeten. Het maken van een meting bedoeld om een definitieve aanwijzing van de plaats van een deeltje te krijgen zal onvermijdelijk zijn impuls beïnvloeden en wat er ook wordt gedaan om dat impuls zo spoedig mogelijk na het meten van zijn positie te meten, de waarschijnlijkheid van welk impuls zal worden ontdekt kan niet anders dan zijn veranderd. Zo kan het onzekerheidsprincipe sommige soorten interferentie verklaren die door onderzoekers worden geproduceerd en die de resultaten van een experiment of een observatie beïnvloeden. Niet alle waarnemerseffecten zijn echter te wijten aan kwantumeffecten of het onzekerheidsprincipe. De rest zijn "waarnemerseffecten" maar geen kwantumonzekerheidseffecten.

Waarnemerseffecten omvatten allerlei zaken die werken op onze gewone menselijke schaal van gebeurtenissen. Als een antropoloog een duidelijk beeld probeert te krijgen van het leven in een primitieve samenleving, maar zijn of haar aanwezigheid verstoort de gemeenschap die hij of zij bezoekt, dan kunnen de gedane waarnemingen zeer misleidend zijn. Geen van de relevante interacties vindt echter plaats op het niveau dat wordt beschreven door de kwantummechanica of het onzekerheidsprincipe.

Soms wordt het woord "quantum" voor reclamedoeleinden gebruikt om iets nieuws en krachtigs aan te duiden. De fabrikant van kleine benzinemotoren, Briggs and Stratton, heeft bijvoorbeeld een lijn van viercilindermotoren met een laag vermogen voor benzinemaaiers en soortgelijk tuingereedschap die zij "Quantum" noemt.

 

Meer lezen

• Inleiding tot de kwantumtheorie, blz. 115 en blz. 158.

J.P. McEvoy en Oscar Zarate