Constante van Planck

Achtergrond

In dit artikel gebruikte symbolen.
Symbool Betekenis E Energie h Constante van Planck k Boltzmann-constante c lichtsnelheid λ stralingsgolflengte ν stralingsfrequentie T absolute temperatuur

Tussen 1670 en 1900 discussieerden wetenschappers over de aard van het licht. Sommige wetenschappers geloofden dat licht bestond uit vele miljoenen kleine deeltjes. Andere wetenschappers geloofden dat licht een golf was.

Licht: golven of deeltjes?

In 1678 schreef Christiaan Huygens het boek Traité de la lumiere ("Verhandeling over licht"). Hij geloofde dat licht bestond uit golven. Hij zei dat licht niet uit deeltjes kon bestaan omdat licht van twee stralen niet tegen elkaar kaatsen. In 1672 schreef Isaac Newton het boek Opticks. Hij geloofde dat licht bestond uit rode, gele en blauwe deeltjes die hij corpusles noemde. Newton verklaarde dit met zijn "twee prisma's experiment". Het eerste prisma verdeelde het licht in verschillende kleuren. Het tweede prisma voegde deze kleuren weer samen tot wit licht.

In de 18e eeuw kreeg de theorie van Newton de meeste aandacht. In 1803 beschreef Thomas Young het "dubbelspletenexperiment". Bij dit experiment interfereert licht dat door twee smalle spleten gaat met zichzelf. Dit veroorzaakt een patroon waaruit blijkt dat licht uit golven bestaat. De rest van de negentiende eeuw kreeg de golftheorie van licht de meeste aandacht. In de jaren 1860 ontwikkelde James Clerk Maxwell vergelijkingen die elektromagnetische straling als golven beschreven.

De theorie van elektromagnetische straling behandelt licht, radiogolven, microgolven en vele andere soorten golven als hetzelfde, behalve dat ze verschillende golflengten hebben. De golflengte van het licht dat wij met onze ogen kunnen zien, ligt ruwweg tussen 400 en 600 nm. De golflengte van radiogolven varieert van 10 m tot 1500 m en de golflengte van microgolven is ongeveer 2 cm. In een vacuüm reizen alle elektromagnetische golven met de lichtsnelheid. De frequentie van de elektromagnetische golf wordt gegeven door:

ν = c λ {{frac {c}{lambda }} .

De symbolen worden hier gedefinieerd.

Zwarte carrosserie-radiatoren

Alle warme dingen geven warmtestraling af, wat elektromagnetische straling is. Voor de meeste dingen op aarde ligt deze straling in het infrarode bereik, maar iets dat heel heet is (1000 °C of meer), geeft zichtbare straling af, dat wil zeggen licht. Eind 1800 bestudeerden veel wetenschappers de golflengten van de elektromagnetische straling van zwarte lichamen bij verschillende temperaturen.

Rayleigh-Jeans recht

Lord Rayleigh publiceerde de grondbeginselen van de wet van Rayleigh-Jeans voor het eerst in 1900. De theorie was gebaseerd op de kinetische theorie van gassen. Sir James Jeans publiceerde een meer volledige theorie in 1905. De wet relateert de hoeveelheid en de golflengte van de elektromagnetische energie die een zwart lichaam bij verschillende temperaturen afgeeft. De vergelijking die dit beschrijft is:

B λ ( T ) = 2 c k T λ 4 {Displaystyle B_{lambda }(T)={frac {2ckT}{lambda ^{4}}}} .

Voor straling met een lange golflengte kwamen de met deze vergelijking voorspelde resultaten goed overeen met de in een laboratorium verkregen praktische resultaten. Voor korte golflengten (ultraviolet licht) was het verschil tussen theorie en praktijk echter zo groot dat het de bijnaam "de ultravioletcatastrofe" kreeg.

Wet van Planck

in 1895 publiceerde Wien de resultaten van zijn onderzoek naar de straling van een zwart lichaam. Zijn formule was:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {displaystyle B_{lambda }(T)={frac {2hc^{2}}{lambda ^{5}}e^{frac {hc}{lambda kT}}}} .

Deze formule werkte goed voor elektromagnetische straling met korte golflengten, maar werkte niet goed bij lange golflengten.

In 1900 publiceerde Max Planck de resultaten van zijn onderzoek. Hij probeerde een uitdrukking te ontwikkelen voor zwartlichaamstraling uitgedrukt in termen van golflengte door aan te nemen dat straling bestond uit kleine kwanta en vervolgens te kijken wat er gebeurde als de kwanta oneindig klein werden gemaakt (dit is een standaard wiskundige benadering). De uitdrukking was:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {displaystyle B_{lambda }(T)={{frac {2hc^{2}}{{lambda ^{5}}}~{frac {1}{e^{frac {hc}{lambda kT}}-1}}} .

Als de golflengte van het licht zeer groot mag worden, dan kan worden aangetoond dat de Raleigh-Jeans en de Planck-relaties vrijwel identiek zijn.

Hij berekende h en k en vond dat

h = 6,55×10⁻²⁷ erg-sec.

k = 1,34×10⁻¹⁶ erg-deg^-1 .

De waarden liggen dicht bij de hedendaagse geaccepteerde waarden van respectievelijk 6,62606×10⁻³⁴ en 1,38065×10⁻¹⁶ . De wet van Planck komt goed overeen met de experimentele gegevens, maar de volledige betekenis ervan werd pas enkele jaren later ingezien.

Kwantumtheorie van licht

Het blijkt dat elektronen door het foto-elektrisch effect worden afgestoten als het licht een drempelfrequentie bereikt. Daaronder kunnen geen elektronen uit het metaal worden uitgezonden. In 1905 publiceerde Albert Einstein een artikel waarin hij het effect verklaarde. Einstein stelde voor dat een lichtstraal geen golf is die zich door de ruimte voortplant, maar eerder een verzameling discrete golfpakketjes (fotonen), elk met energie. Einstein zei dat het effect werd veroorzaakt doordat een foton een elektron trof. Dit toonde het deeltjeskarakter van licht aan.

Einstein ontdekte ook dat elektromagnetische straling met een lange golflengte geen effect had. Einstein zei dat dit kwam omdat de "deeltjes" niet genoeg energie hadden om de elektronen te verstoren.

Planck stelde voor dat de energie van elk foton gerelateerd was aan de frequentie van het foton door de constante van Planck. Dit kan wiskundig worden geschreven als:

E = h ν = h c λ {displaystyle E=h ν ={{frac {hc}{lambda }}} .

Planck ontving de Nobelprijs in 1918 als erkenning voor zijn diensten aan de vooruitgang van de fysica door zijn ontdekking van energiequanta. In 1921 ontving Einstein de Nobelprijs omdat hij de constante van Planck in verband bracht met het foto-elektrisch effect.

 
Solway Conferentie 1911. Planck, Einstein en Jeans staan. Planck is tweede van links. Einstein is tweede van rechts. Jeans is vijfde van rechts. Wien zit, derde van rechts.  


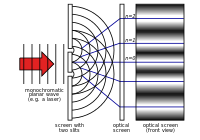
Young's dubbele spleet experiment  


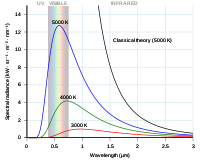
Rayleigh-Jeans curve en Planck's curve uitgezet tegen de golflengte van de fotonen.  


Illustratie uit Newtons originele brief aan de Royal Society (1 januari 1671 [Juliaanse kalender]). S stelt zonlicht voor. Het licht tussen de vlakken BC en DE is in kleur. Deze kleuren worden gerecombineerd om zonlicht op het vlak GH te vormen.  

Toepassing

De constante van Planck is van belang voor vele toepassingen. Hieronder volgen er enkele.

Bohr-model van het atoom

In 1913 publiceerde Niels Bohr het Bohr-model van de structuur van een atoom. Bohr stelde dat het impulsmoment van de elektronen die rond de kern draaien, slechts bepaalde waarden kan hebben. Deze waarden worden gegeven door de vergelijking

L = n h 2 π {Displaystyle L=n{{frac {h}{2\pi }}}

waarbij

L = het impulsmoment van een niveau.

n = positief geheel getal.

h = constante van Planck.

Het Bohr-model van het atoom kan worden gebruikt om de energie van elektronen op elk niveau te berekenen. Normaal vullen elektronen de laagst genummerde toestanden van een atoom op. Als het atoom energie ontvangt van bijvoorbeeld een elektrische stroom, worden de elektronen in een hogere toestand gebracht. De elektronen vallen dan terug naar een lagere toestand en verliezen hun extra energie door een foton af te geven. Omdat de energieniveaus specifieke waarden hebben, zullen de fotonen specifieke energieniveaus hebben. Licht dat op deze manier wordt uitgezonden, kan met behulp van een prisma in verschillende kleuren worden gesplitst. Elk element heeft zijn eigen patroon. Het patroon voor neon is hiernaast afgebeeld.

Het onzekerheidsprincipe van Heisenberg

In 1927 publiceerde Werner Heisenberg het onzekerheidsprincipe. Het principe stelt dat het niet mogelijk is een meting te doen zonder het gemetene te verstoren. Het stelt ook een grens aan de minimale verstoring die een meting veroorzaakt.

In de macroscopische wereld maken deze verstoringen weinig verschil. Als bijvoorbeeld de temperatuur van een vloeistofkolf wordt gemeten, zal de thermometer een kleine hoeveelheid energie absorberen wanneer deze opwarmt. Dit veroorzaakt een kleine fout in de uiteindelijke aflezing, maar deze fout is klein en niet belangrijk.

In de kwantummechanica liggen de zaken anders. Sommige metingen worden gedaan door te kijken naar het patroon van verstrooide fotonen. Een voorbeeld hiervan is de Comptonverstrooiing. Als zowel de positie als het momentum van een deeltje wordt gemeten, stelt het onzekerheidsprincipe dat er een afruil is tussen de nauwkeurigheid waarmee het momentum wordt gemeten en de nauwkeurigheid waarmee de positie wordt gemeten. De vergelijking die deze afweging beschrijft is:

Δ x Δ p ⩾ h 4 π {Displaystyle \\Delta x,\Delta p \geqslant {\frac {h}{4\pi }}}.

waarbij

Δp = onzekerheid in momentum.

Δx = onzekerheid in positie.

h = constante van Planck.

Kleur van lichtgevende diodes

In de elektrische schakeling hiernaast is de spanningsval over de lichtgevende diode (LED) afhankelijk van het materiaal van de LED. Voor siliciumdiodes is de daling 0,6 V. Voor LED's ligt de daling echter tussen 1,8 V en 2,7 V. Met deze informatie kan de gebruiker de constante van Planck berekenen.

De energie die nodig is voor één elektron om over de potentiële barrière in het LED-materiaal te springen wordt gegeven door

E = Q e V L {Displaystyle E=Q_{e}V_{L},}.

waarbij

Q_e is de lading van één elektron.

V_L is de spanningsval over de LED.

Wanneer het elektron weer vervalt, zendt het één foton licht uit. De energie van het foton wordt gegeven door dezelfde vergelijking die wordt gebruikt bij het foto-elektrisch effect. Als deze vergelijkingen worden gecombineerd, zijn de golflengte van het licht en de spanning aan elkaar gerelateerd door

λ = h c V L Q e {\lambda ={frac {hc}{V_{L}Q_{e}}}}.

Uit deze relatie kan de onderstaande tabel worden berekend.

Kleur	Golflengte (nm)	Spanning
rood licht	650	1.89
groen licht	550	2.25
blauw licht	470	2.62

 
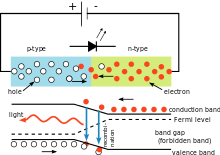
Eenvoudige LED-schakeling die het gebruik van de constante van Planck illustreert. De kleur van het uitgestraalde licht hangt af van de spanningsval over de diode. De golflengte van het licht kan worden berekend met behulp van de constante van Planck.  


Zichtbaar spectrum van neon. Elke lijn vertegenwoordigt een ander paar energieniveaus.  


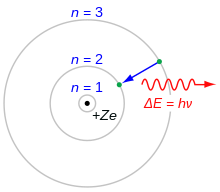
Bohr's model van het atoom. Een elektron dat van de n=3 schil naar de n=2 schil valt, verliest energie. Deze energie wordt meegenomen als een enkel foton.  

Waarde van de constante van Planck en de herdefinitie van de kilogram

Sinds de ontdekking ervan zijn de metingen van h veel beter geworden. Planck schatte de waarde van h voor het eerst op 6,55×10⁻²⁷ erg-sec. Deze waarde ligt binnen 5% van de huidige waarde.

Per 3 maart 2014 is de beste meting van h in SI-eenheden 6,62606957×10⁻³⁴ J-s. Het equivalent in cgs-eenheden is 6,62606957×10⁻²⁷ erg-sec. De relatieve onzekerheid van h is 4,4×10⁻⁸ .

De gereduceerde constante van Planck (ħ) is een waarde die soms wordt gebruikt in de kwantummechanica. Hij wordt gedefinieerd door

ℏ = h 2 π {displaystyle hbar ={{frac {h}{2\pi }}} .

In de kwantummechanica worden soms Planck-eenheden gebruikt in plaats van SI. In dit systeem heeft de gereduceerde constante van Planck een waarde van 1, dus de waarde van de constante van Planck is 2π.

Plancks constante kan nu zeer nauwkeurig worden gemeten. Dit heeft het BIPM ertoe gebracht een nieuwe definitie van de kilogram te overwegen. Het internationale prototype kilogram wordt niet langer gebruikt om de kilogram te definiëren. In plaats daarvan bepaalt het BIPM dat de constante van Planck een exacte waarde heeft. Wetenschappers gebruiken deze waarde en de definities van de meter en de seconde om de kilogram te definiëren.

 

Waarde van de theoretische constante van Planck

De constante van Planck kan ook wiskundig worden afgeleid:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {{displaystyle h={{frac {mu _{0}pi }{12c^{3}}{[{q_{0}}{ 0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}}=6.63 maal 10^{-34}J ⋅ s}

Hierbij is μ 0 {{0} de permeabiliteit van de vrije ruimte, c {{0} de lichtsnelheid, q 0 {{0}} de elektrische lading van het elektron, a 0 {\displaystyle a_{0}} is de straal van Bohr, en f 1 r {\displaystyle f_{1r}} is de omwentelingsfrequentie van het elektron in een waterstofatoom ( f 1 r = 3.29 × 10 15 r e v / s ) {{displaystyle (f_{1r}=3.29 maal 10^{15}rev/s)} . Wanneer deze constante waarden worden toegevoegd aan de theoretische Planck-constante, is de theoretische Planck-constante waarde precies gelijk aan de experimentele waarde.

 De elementaire formule van de constante van Planck in termen van de verhouding proton/elektron-massa, de lading van het elektron, de lichtsnelheid en de permittiviteit van het vacuüm is afgeleid in. Deze wordt als volgt uitgedrukt:

h = e 2 c ε 0 π 2 3 m p m e {{displaystyle h={{frac {e^{2}}{c,varepsilon _{0}}}{{{frac {m_{p}}{m_{e}}}}}}

waarbij e {\displaystyle e} de elementaire lading van een elektron is, m p {\displaystyle m_{p}} de massa van een proton, m e {\displaystyle m_{e}} de massa van een elektron, ε 0 {\displaystyle \varepsilon _{0}} de permeabiliteit van het vacuüm, en c {\displaystyle c} de lichtsnelheid.

 

Gerelateerde pagina's

• Golf-deeltje dualiteit