Heisenberg's onzekerheidsprincipe | de belangrijkste resultaten van de twintigste eeuwse fysica

Verwarring met waarnemerseffect

Historisch gezien is het onzekerheidsprincipe verward met een enigszins vergelijkbaar effect in de natuurkunde, het zogenaamde waarnemerseffect. Dit zegt dat metingen aan sommige systemen niet kunnen worden verricht zonder de systemen te beïnvloeden. Heisenberg bood een dergelijk waarnemerseffect op het kwantumniveau aan als een fysische "verklaring" van de kwantumonzekerheid.

Nochtans, is het nu duidelijk dat het onzekerheidsprincipe een eigenschap van alle golf-als systemen is. Het ontstaat in de kwantummechanica eenvoudigweg door de materie-golf aard van alle kwantumobjecten. Aldus, stelt het onzekerheidsprincipe eigenlijk een fundamentele eigenschap van quantumsystemen, en is geen verklaring over het waarnemingssucces van huidige technologie. "Meting" betekent niet alleen een proces waaraan een fysicus-waarnemer deelneemt, maar eerder elke interactie tussen klassieke en kwantumobjecten ongeacht een waarnemer.

 

Het idee van onbepaaldheid

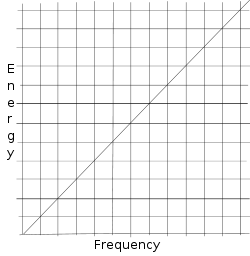
Het onzekerheidsprincipe kwam voort uit de matrixmechanica van Werner Heisenberg. Max Planck wist al dat de energie van een lichteenheid evenredig is met de frequentie van die lichteenheid ( E ∝ ν {Displaystyle Epropto \nu } ), en dat de hoeveelheid energie kan worden uitgedrukt in bekende termen zoals de joule door een evenredigheidsconstante te gebruiken. De constante die hij de wereld gaf, heet nu de constante van Planck en wordt weergegeven met de letter h. Wanneer matrices worden gebruikt om kwantummechanica uit te drukken, moeten vaak twee matrices worden vermenigvuldigd om een derde matrix te krijgen die het antwoord geeft dat de natuurkundige probeert te vinden. Maar een matrix zoals P (voor momentum) vermenigvuldigen met een matrix zoals X (voor positie) geeft een andere antwoordmatrix dan de matrix die u krijgt als u X vermenigvuldigt met P. Het resultaat van het vermenigvuldigen van P met X en X met P en het vervolgens vergelijken ervan heeft altijd de constante van Planck als factor. Het getal dat wordt gebruikt om de constante van Planck te schrijven, hangt altijd af van het gebruikte meetsysteem. (Bij een bepaald meetsysteem is de numerieke waarde ervan één.) De helling van de lijn in het diagram rechts, die de verhouding tussen frequentie en energie weergeeft, hangt ook af van het gekozen meetsysteem.

De volgende diagrammen laten zien wat er gebeurt als we zowel locatie als momentum proberen te meten.

Het praktische resultaat van deze wiskundige ontdekking is dat wanneer een fysicus de positie duidelijker maakt, het momentum minder duidelijk wordt, en dat wanneer de fysicus het momentum duidelijker maakt, de positie minder duidelijk wordt. Heisenberg zei dat de dingen "onbepaald" zijn, en anderen zeiden graag dat ze "onzeker" waren. Maar de wiskunde laat zien dat het de dingen in de wereld zijn die onbepaald of "vaag" zijn, en niet dat het alleen maar zo is dat mensen onzeker zijn over wat er gebeurt.

 
Door de opening in het midden op te hangen met veren kan het momentum worden gemeten, maar wordt de opening onvoorspelbaar verplaatst, zodat informatie over de locatie van het foton in het midden verloren gaat.  


Gat met veer meet momentum  


Smal gat, diffuse focus  


Door de opening te verkleinen wordt de zekerheid over waar het foton zich in het midden bevindt groter, maar de richting van daar naar het detectiescherm rechts wordt navenant onzekerder.  


Breed gat, scherpe focus  



 

Onbepaaldheid in wiskundige vorm gieten

Hier zullen wij de eerste vergelijking tonen die het basisidee gaf dat later in het onzekerheidsprincipe van Heisenberg wordt getoond.

Heisenbergs baanbrekende paper van 1925 maakt geen gebruik van matrices en vermeldt ze zelfs niet. Heisenbergs grote succes was de "regeling die in principe in staat was om uniek de relevante fysieke kwaliteiten (overgangsfrequenties en amplitudes) te bepalen" van waterstofstraling.

Nadat Heisenberg zijn doorbraakdocument had geschreven, gaf hij het aan een van zijn leraren om het op te knappen en ging op vakantie. Max Born was verbaasd over de vergelijkingen en de niet-commuterende vergelijkingen die zelfs Heisenberg een probleem vond. Na enkele dagen besefte Born dat deze vergelijkingen aanwijzingen waren voor het uitschrijven van matrices. Matrices waren nieuw en vreemd, zelfs voor wiskundigen uit die tijd, maar hoe je ermee moest rekenen was al duidelijk bekend. Hij en een paar anderen werkten alles uit in matrixvorm voordat Heisenberg terugkwam van zijn verlof, en binnen een paar maanden vormde de nieuwe kwantummechanica in matrixvorm de basis voor een ander artikel.

Max Born zag dat wanneer de matrices die pq en qp vertegenwoordigen werden berekend, ze niet gelijk zouden zijn. Heisenberg had hetzelfde al gezien in termen van zijn oorspronkelijke manier van opschrijven, en Heisenberg kan geraden hebben wat bijna onmiddellijk duidelijk was voor Born - dat het verschil tussen de antwoordmatrices voor pq en voor qp altijd twee factoren zou betreffen die uit Heisenbergs oorspronkelijke wiskunde kwamen: Planck's constante h en i, wat de vierkantswortel is van negatief één. Dus het idee van wat Heisenberg liever het "onbepaaldheidsprincipe" noemde (meestal bekend als het onzekerheidsprincipe) zat verborgen in Heisenbergs oorspronkelijke vergelijkingen.

Heisenberg had gekeken naar veranderingen die gebeuren in een atoom wanneer een elektron zijn energieniveau verandert en dus dichter bij het centrum van zijn atoom komt of verder van het centrum komt, en, vooral, situaties waarin een elektron in twee stappen naar een lagere energietoestand valt. Max Born legde uit hoe hij het vreemde "recept" van Heisenberg nam voor het vinden van het product, C, van een verandering in een atoom van energieniveau n naar energieniveau n-b, waarbij de som werd genomen van de vermenigvuldiging van een verandering in iets genaamd A (dat bijvoorbeeld de frequentie van een foton zou kunnen zijn), geproduceerd door een verandering in de energie van een elektron in het atoom tussen energietoestand n en energietoestand n-a) met een volgende verandering in iets genaamd B (dat bijvoorbeeld de amplitude van een verandering zou kunnen zijn), geproduceerd door een andere verandering in de energietoestand van n-a naar n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {C(n,n-b)=sum _{a}^{},A(n,n-a)B(n-a,n-b)}.

en ontdekte iets baanbrekends:

Door overweging van ...voorbeelden...[Heisenberg] vond deze regel.... Dit was in de zomer van 1925. Heisenberg...nam verlof...en overhandigde zijn paper aan mij voor publicatie....

Heisenberg's regel van vermenigvuldiging liet me geen rust, en na een week van intensief denken en proberen, herinnerde ik me plotseling een algebraïsche theorie....Such quadratische arrays zijn heel bekend bij wiskundigen en heten matrices, in combinatie met een definitieve regel van vermenigvuldiging. Ik paste deze regel toe op de kwantumvoorwaarde van Heisenberg en ontdekte dat deze overeenkwam voor de diagonale elementen. Het was gemakkelijk te raden wat de overige elementen moesten zijn, namelijk nul; en onmiddellijk stond er voor mij de vreemde formule

Q P - P Q = i h 2 π {QP-PQ={frac {ih}{2pi }}}}
 [Het symbool Q is de matrix voor verplaatsing, P is de matrix voor momentum, i staat voor de vierkantswortel van negatief, en h is de constante van Planck].

Later verwerkte Heisenberg zijn ontdekking in een andere wiskundige vorm:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x,\Delta p \geq {{2}}}.

(Het speciale symbool ℏ {hbar} wordt "h-bar" genoemd, of "gereduceerde Planks-constante", is gelijk aan h 2 π {frac {h}{2\pi }} .)

De wiskunde is een manier om dingen te beschrijven die in de echte wereld gebeuren. U zou kunnen denken dat het gemakkelijk is om zowel de exacte positie van iets als de exacte massa, baan en snelheid ervan te bepalen. In werkelijkheid moet u echter twee dingen doen om uw antwoord te krijgen. Als u de positie en het momentum meet van een kogel die ergens in een rotswand van een grote berg vastzit, is het een eenvoudige zaak. De berg lijkt nergens heen te gaan, en de kogel ook niet. Zijn positie is dus bekend en zijn snelheid is 0, dus zijn momentum is ook 0. Maar als de kogel zich ergens tussen een geweer en een doelwit bevindt, zal het moeilijk zijn om zijn positie op een bepaald moment te bepalen. Het beste wat we kunnen doen is een foto maken met een camera met een zeer snelle sluiter. Maar een enkele druk op de sluiter levert slechts één ding op: de positie van de kogel op tijdstip t. Om het momentum te bepalen, zouden we een blok paraffine in de weg van de kogel kunnen leggen en meten hoe het blok paraffine bewoog toen het de kogel tegenhield. Of, als we de massa van de kogel kennen, kunnen we een reeks van twee foto's nemen en de snelheid berekenen door het verschil te kennen tussen de twee posities van de kogel en de tijd tussen de twee verschijningen. Hoe we het ook doen, we moeten de massa, de positie en de tijd tussen twee verschijningen meten. Uiteindelijk moeten we minstens twee metingen doen om tot x en p te komen. In dat geval moeten we kiezen welke meting we eerst doen, en welke als tweede. Het lijkt geen verschil te maken in welke volgorde onze metingen worden gedaan. De massa van de kogel meten en dan twee keer zijn posities meten, of twee keer de posities van de kogel meten en dan de kogel terughalen en zijn massa meten, maakt toch geen verschil? We hebben immers niets met de kogel gedaan wanneer we hem wegen of wanneer we er foto's van maken.

Op de zeer kleine schaal, wanneer we iets als een elektron meten, doet elke meting er echter iets mee. Als we eerst de positie meten, dan veranderen we daarbij het momentum. Als we eerst het momentum van het elektron meten, dan veranderen we daarbij zijn positie. Onze hoop zou zijn om één van hen te meten en dan de andere te meten alvorens om het even wat veranderde, maar onze meting zelf maakt een verandering, en het beste dat wij kunnen hopen te doen is de energie te verminderen die wij aan het elektron bijdragen door het te meten. Die minimale hoeveelheid energie heeft de constante van Planck als een van de factoren.

 

Onzekerheid gaat verder dan matrixwiskunde

Het onzekerheidsprincipe van Heisenberg werd gevonden in de vroegste vergelijkingen van de "nieuwe" kwantumfysica, en de theorie werd gegeven met behulp van matrixwiskunde. Het onzekerheidsprincipe is echter een feit in de natuur, en het duikt op in andere manieren om over kwantumfysica te praten, zoals de vergelijkingen van Erwin Schrödinger.

 

Onbepaaldheid in de natuur, niet de onzekerheid van de mens

Er zijn twee heel verschillende manieren om te kijken naar wat Heisenberg ontdekte: Sommige mensen denken dat de dingen die in de natuur gebeuren "vaststaand" zijn, dat wil zeggen dat de dingen gebeuren volgens een vaste regel, en als we alles zouden weten wat we moeten weten, zouden we altijd kunnen zeggen wat er daarna zal gebeuren. Andere mensen denken dat de dingen die in de natuur gebeuren alleen worden geleid door waarschijnlijkheid, en dat we alleen kunnen weten hoe de dingen zich gemiddeld zullen gedragen - maar dat weten we heel precies.

De natuurkundige John Stewart Bell ontdekte een manier om te bewijzen dat de eerste manier niet juist kan zijn. Zijn werk wordt Bell's stelling of Bell's ongelijkheid genoemd.

 

Populaire cultuur

De uitdrukking "kwantumsprong" of "kwantumdraai" wordt vaak gebruikt in hyperbolische uitdrukkingen door politici en verkoopcampagnes in de massamedia. In de kwantummechanica wordt de term gebruikt om de overgang van een elektron van de ene baan rond de kern van een atoom naar een andere baan, hoger of lager, te beschrijven.

Soms wordt het woord "kwantum" gebruikt in de namen van commerciële producten en bedrijven. Zo produceert Briggs and Stratton vele soorten kleine benzinemotoren voor grasmaaiers, grondfrezen en andere dergelijke kleine machines. Een van hun modelnamen is "Quantum".

Omdat het onzekerheidsprincipe ons vertelt dat bepaalde metingen op atomair niveau niet kunnen worden uitgevoerd zonder andere metingen te verstoren, gebruiken sommigen dit idee om gevallen in de menselijke wereld te beschrijven waarin de activiteit van een waarnemer het ding dat wordt bekeken verandert. Een antropoloog kan naar een verre plaats gaan om te leren hoe de mensen daar leven, maar het feit dat een vreemde persoon uit de buitenwereld hen gadeslaat, kan de manier waarop die mensen handelen veranderen.

Dingen die mensen doen terwijl zij dingen waarnemen die veranderen wat wordt waargenomen, zijn gevallen van het waarnemerseffect. Sommige dingen die mensen doen veroorzaken veranderingen op het zeer kleine niveau van atomen en zijn gevallen van onzekerheid of onbepaaldheid zoals voor het eerst beschreven door Heisenberg. Het onzekerheidsprincipe toont aan dat er altijd een grens is aan hoe klein wij bepaalde meetparen kunnen maken, zoals positie en snelheid of baan en momentum. Het waarnemerseffect zegt dat soms wat mensen doen bij het observeren van dingen, bv. leren over een mierenkolonie door deze op te graven met tuingereedschap, grote effecten kan hebben die veranderen waarover zij probeerden te leren.