Logaritmische spiraal (Spira mirabilis): definitie en voorbeelden
Ontdek de logaritmische spiraal (Spira mirabilis): definitie, geschiedenis met Descartes & Bernoulli en duidelijke voorbeelden uit de natuur. Lees meer.
Een logaritmische spiraal, ook wel gelijkzijdige spiraal of groeispiraal, is een speciaal soort spiraalkromme die vaak in de natuur voorkomt. De logaritmische spiraal werd voor het eerst beschreven door Descartes en later uitgebreid onderzocht door Jakob Bernoulli, die hem Spira mirabilis noemde, "de wonderbaarlijke spiraal".
Definitie en vergelijking
In poolcoördinaten (r, θ) wordt de logaritmische spiraal vaak gegeven door de vergelijking
r(θ) = a · e^{bθ},
waarin a > 0 een positiere schaalfactor is en b een reële constante die de "snelheid" van uitgroei bepaalt. In cartesische coördinaten leidt dit tot de parametrisatie
x(θ) = a · e^{bθ} cos θ,
y(θ) = a · e^{bθ} sin θ.
Belangrijke eigenschappen volgen direct uit deze vorm: na een draaiing Δθ neemt de straal r toe met de factor e^{bΔθ}. Een volledige omwenteling (Δθ = 2π) geeft dus een vergrotingsfactor e^{2πb}.
Constante hoek en zelfgelijkheid
- De logaritmische spiraal is een equiangular of gelijkhoekige spiraal: de hoek α tussen de straalvector (van de oorsprong naar een punt op de spiraal) en de raaklijn in dat punt is constant over de hele kromme. Voor r = a e^{bθ} geldt: tan α = 1 / b, dus α = arctan(1/b).
- Zelfgelijkheid: door rotatie en gelijktijdige schaalvergroting gaat de spiraal in zichzelf over. Dat wil zeggen, roteren over een hoek Δθ komt overeen met vermenigvuldiging van r met e^{bΔθ} — de vorm verandert niet, alleen de schaal.
- Als b > 0 spitst de spiraal zich naar buiten toe toe; voor b < 0 draait de spiraal naar de oorsprong als θ toeneemt.
Vergelijking met andere spiralen
- Archimedes' spiraal heeft de vorm r = a + cθ: de afstand tussen opeenvolgende windingen is constant. Bij de logaritmische spiraal neemt die afstand geometrisch toe, niet lineair.
- De zogenaamde 'gulden spiraal' (golden spiral) is een logaritmische spiraal waarvoor de vergrotingsfactor over een kwartslag gelijk is aan de gulden verhouding φ ≈ 1,618. Voor die spiraal geldt b = (2 ln φ) / π.
Voorbeelden in natuur en techniek
- Schelpen en slakkenhuizen: veel schelpen vertonen een spiraalvormige groei die goed benaderd kan worden door een logaritmische spiraal.
- Spiraalarmen van sterrenstelsels: de armen van sommige sterrenstelsels volgen ongeveer logarithmische spiralen, doordat rotatie en zelforganiserende processen samenwerken.
- Weersverschijnselen: orkanen en wervelstormen tonen spiraalvormige wolkenpatronen die vaak aan logarithmische spiralen doen denken.
- Planten en phyllotaxis: de rangschikking van bladeren, zaden en schubben (bijvoorbeeld bij dennenappels of zonnebloemen) produceert vaak reeksen spiralen en patronen die met logaritmische spiralen en de gulden verhouding in verband worden gebracht.
- Techniek en architectuur: logaritmische spiralen worden soms toegepast wanneer een ontwerp zelfgelijkend moet blijven bij schaling, of voor esthetische patronen.
Enkele aanvullende eigenschappen
- Asymptotisch gedrag: voor b > 0 nadert de spiraal de oorsprong als θ → −∞ en groeit zonder begrenzing als θ → +∞; omgekeerd voor b < 0.
- Lengte en kromming: er bestaan expliciete formules voor kromming en booglengte van delen van de spiraal, maar die zijn technischer van aard en afhankelijk van de parameter b.
Korte historische noot
Jakob Bernoulli was zo onder de indruk van deze kromme dat hij haar "Spira mirabilis" noemde en wilde dat ze op zijn grafsteen zou komen met het motto Eadem mutata resurgo ("Veranderd, stijg ik toch weer hetzelfde op"). De specifieke wiskundige eigenschappen en de vele toepassingen in de natuur maakten de logaritmische spiraal tot een klassiek onderwerp in de meetkunde en de natuurwetenschappen.

De armen van spiraalstelsels hebben vaak de vorm van een logaritmische spiraal, hier het Draaikolkstelsel.

Een lagedrukgebied boven IJsland vertoont een ongeveer logaritmisch spiraalpatroon.
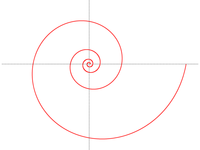
Logaritmische spiraal (steek 10°)

Uitsnede van een nautilusschelp met de kamers in een ongeveer logaritmische spiraal.
Definitie
In poolcoördinaten (r, θ) kan de kromme worden geschreven als
r = a e b θ {Displaystyle r=ae^{b theta },}
of
θ = 1 b ln ( r / a ) , {frac {1}{b}}{ln(r/a),}.
vandaar de naam "logaritmisch". In parametrische vorm is de kromme
x ( t ) = r cos ( t ) = a e b t cos ( t ) {\displaystyle x(t)=r\cos(t)=ae^{bt}\cos(t)\,}
y ( t ) = r sin ( t ) = a e b t sin ( t ) {\displaystyle y(t)=r rsin(t)=ae^{bt}sin(t)¦.}
met reële getallen a en b.
De spiraal heeft de eigenschap dat de hoek ɸ tussen de raaklijn en de radiale lijn in het punt (r,θ) constant is. Deze eigenschap kan in differentiaalmeetkundige termen worden uitgedrukt als
arccos ⟨ r ( θ ) , r ′ ( θ ) ⟩ ‖ r ( θ ) ‖ ‖ r ′ ( θ ) ‖ = arctan 1 b = ϕ , {\displaystyle \arccos {\mathbf {r} (\theta ),\mathbf {r} (\theta )\mathbf {r} (\theta )\mathbf {r} (\theta )\r}=arctan {frac {1}{b}}=\phi, }
De afgeleide r'(θ) is evenredig met de parameter b. Met andere woorden, deze bepaalt hoe "dicht" en in welke richting de spiraal zich spiraalt. In het extreme geval dat b = 0 (ɸ = π/2) wordt de spiraal een cirkel met straal a. Omgekeerd, in de limiet dat b het oneindige nadert (ɸ → 0) neigt de spiraal naar een rechte lijn. Het complement van ɸ wordt de steek genoemd.
Spira mirabilis en Jakob Bernoulli
Spira mirabilis, Latijn voor "wonderbaarlijke spiraal", is een andere naam voor de logaritmische spiraal. Hoewel deze kromme al door andere wiskundigen was genoemd, werd de naam "miraculeuze" of "wonderbaarlijke" spiraal aan deze kromme gegeven door Jakob Bernoulli, omdat hij gefascineerd was door een van de unieke wiskundige eigenschappen ervan: de grootte van de spiraal neemt toe, maar de vorm blijft dezelfde bij elke toegevoegde kromme. Misschien vanwege deze eigenschap is de spira mirabilis in de natuur geëvolueerd, gezien in sommige levende wezens, zoals nautilusschelpen en zonnebloemkoppen. Jakob Bernoulli wilde de vorm op zijn grafsteen, maar bij vergissing werd daar een Archimedische spiraal geplaatst.
Logaritmische spiralen in de natuur
In verschillende natuurverschijnselen kan men krommen vinden die bijna logaritmische spiralen zijn. Hier volgen enkele voorbeelden en redenen:
- De nadering van een havik naar zijn prooi. Hun scherpste zicht is in een hoek ten opzichte van hun vliegrichting; deze hoek is dezelfde als de spiraalsteek.
- De nadering van een insect tot een lichtbron. Ze zijn eraan gewend dat de lichtbron een constante hoek vormt met hun vliegroute. Meestal is de zon de enige lichtbron en op die manier vliegen levert een vrijwel rechte lijn op.
- De armen van spiraalstelsels. Ons eigen melkwegstelsel, de Melkweg, zou vier grote spiraalarmen hebben, die elk ruwweg een logaritmische spiraal zijn met een verticale hoek van ongeveer 12 graden, een ongewoon kleine verticale hoek voor een melkwegstelsel als de Melkweg. In het algemeen hebben armen in spiraalstelsels een verticale hoek van ongeveer 10 tot 40 graden.
- De armen van tropische cyclonen, zoals orkanen.
|
|
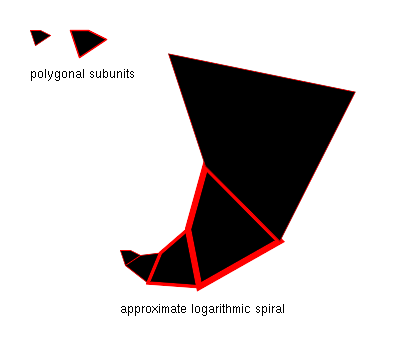
- Veel biologische structuren, waaronder spinnenwebben en de schelpen van weekdieren. In deze gevallen is de reden de volgende: Begin met een onregelmatig gevormde tweedimensionale figuur F0 . Breid F0 uit met een bepaalde factor om F1 te krijgen, en plaats F1 naast F0 , zodat twee zijden elkaar raken. Breid nu F1 uit met dezelfde factor om F2 te krijgen, en plaats deze naast F1 zoals voorheen. Door dit te herhalen ontstaat bij benadering een logaritmische spiraal waarvan de steek wordt bepaald door de uitzettingsfactor en de hoek waarmee de figuren naast elkaar zijn geplaatst. Dit wordt voor veelhoekige figuren getoond in de bijgaande grafiek.
Gerelateerde pagina's
- Fibonacci reeks
- Veerbelaste nokbeveiliging
Zoek in de encyclopedie