Oppervlaktespanning | effect waarbij het oppervlak van een vloeistof sterk is
Oppervlaktespanning is een effect waarbij het oppervlak van een vloeistof sterk is. Het oppervlak kan een gewicht omhoog houden, en het oppervlak van een waterdruppel houdt de druppel bij elkaar, in de vorm van een bal. Sommige kleine dingen kunnen door oppervlaktespanning op een oppervlak drijven, ook al zouden ze normaal niet kunnen drijven. Sommige insecten (bv. schaatsenrijders) kunnen hierdoor op het wateroppervlak lopen. Deze eigenschap wordt veroorzaakt doordat de moleculen in de vloeistof elkaar aantrekken (cohesie), en is verantwoordelijk voor veel gedragingen van vloeistoffen.
Oppervlaktespanning heeft de dimensie van kracht per lengte-eenheid, of van energie per oppervlakte-eenheid. De twee zijn gelijkwaardig, maar wanneer men het heeft over energie per oppervlakte-eenheid, gebruikt men de term oppervlakte-energie - een meer algemene term in die zin dat hij ook van toepassing is op vaste stoffen en niet alleen op vloeistoffen.
In de materiaalkunde wordt oppervlaktespanning gebruikt voor ofwel oppervlaktespanning ofwel vrije oppervlakte-energie.
Veroorzaakt
De cohesiekrachten tussen de vloeistofmoleculen veroorzaken oppervlaktespanning. In de bulk van de vloeistof wordt elk molecuul in alle richtingen evenveel aangetrokken door naburige vloeistofmoleculen, waardoor de nettokracht nul is. De moleculen aan het oppervlak hebben geen andere moleculen aan alle kanten en worden daarom naar binnen getrokken. Dit creëert enige interne druk en dwingt vloeistofoppervlakken samen te trekken tot het minimale oppervlak.
Oppervlaktespanning is verantwoordelijk voor de vorm van vloeistofdruppels. Hoewel ze gemakkelijk vervormen, hebben waterdruppels de neiging om in een bolvorm te worden getrokken door de cohesiekrachten van de oppervlaktelaag. Zonder andere krachten, waaronder de zwaartekracht, zouden druppels van vrijwel alle vloeistoffen perfect bolvormig zijn. De bolvorm minimaliseert de noodzakelijke "wandspanning" van de oppervlaktelaag volgens de wet van Laplace.
Een andere manier om het te bekijken is in termen van energie. Een molecuul in contact met een buur bevindt zich in een lagere energietoestand dan wanneer het alleen zou zijn (niet in contact met een buur). De binnenste moleculen hebben zoveel buren als ze maar kunnen hebben, maar de grensmoleculen missen buren (vergeleken met de binnenste moleculen). De grensmoleculen hebben dus een hogere energie. Om de energietoestand van de vloeistof te minimaliseren, moet het aantal grensmoleculen met een hogere energie geminimaliseerd worden. De geminimaliseerde hoeveelheid grensmoleculen resulteert in een geminimaliseerde oppervlakte.
Als gevolg van het minimaliseren van de oppervlakte zal een oppervlak de meest gladde vorm aannemen die het kan aannemen. Elke kromming in de vorm van het oppervlak leidt tot een groter oppervlak en een hogere energie. Het oppervlak duwt dus terug tegen elke kromming, net zoals een bal die bergop wordt geduwd, terugduwt om zijn gravitationele potentiële energie te minimaliseren.
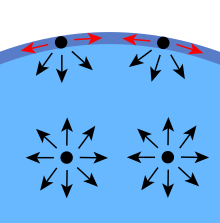
Schema van de krachten op moleculen in vloeistof

De oppervlaktespanning voorkomt dat de paperclip onder water komt.
Effecten in het dagelijks leven
Water
Bestudering van water laat verschillende effecten van oppervlaktespanning zien:
A. Regenwater vormt parels op het oppervlak van een wasachtig oppervlak, zoals een blad. Water hecht zich zwak aan was en sterk aan zichzelf, dus clustert het water in druppels. Door de oppervlaktespanning krijgen ze hun bijna-bolvorm, omdat een bol de kleinst mogelijke verhouding tussen oppervlakte en volume heeft.
B. Druppelvorming ontstaat wanneer een vloeistofmassa wordt uitgerekt. De animatie laat zien hoe water dat aan de kraan blijft kleven aan massa wint totdat het wordt uitgerekt tot een punt waarop de oppervlaktespanning het niet langer aan de kraan kan binden. Het scheidt zich dan af en de oppervlaktespanning vormt de druppel tot een bol. Als er een waterstroom uit de kraan zou lopen, zou de stroom tijdens de val in druppels uiteenvallen. De zwaartekracht rekt de stroom uit, waarna de oppervlaktespanning hem in bollen knijpt.
C. Voorwerpen die dichter zijn dan water blijven drijven wanneer ze niet bevochtigbaar zijn en hun gewicht klein genoeg is om gedragen te worden door de krachten van de oppervlaktespanning. Schaatsenrijders gebruiken bijvoorbeeld de oppervlaktespanning om over het oppervlak van een vijver te lopen. Het wateroppervlak gedraagt zich als een elastische film: de poten van het insect veroorzaken inkepingen in het wateroppervlak, waardoor het oppervlak toeneemt.
D. De scheiding van olie en water (in dit geval water en vloeibare was) wordt veroorzaakt door een spanning in het oppervlak tussen ongelijke vloeistoffen. Dit type oppervlaktespanning wordt "grensvlakspanning" genoemd, maar de fysica ervan is dezelfde.
E. Tranen van wijn is de vorming van druppels en stroompjes op de zijkant van een glas met een alcoholische drank. De oorzaak is een complexe interactie tussen de verschillende oppervlaktespanningen van water en ethanol. Het wordt veroorzaakt door een combinatie van wijziging van de oppervlaktespanning van water door ethanol en het feit dat ethanol sneller verdampt dan water.
· 
A. Water parelt op een blad
· 
B. Water dat uit een kraan druppelt
· 
C. Schaatsers blijven boven op de vloeistof door oppervlaktespanning
· 
D. Lavalamp met interactie tussen ongelijke vloeistoffen; water en vloeibare was
· 
E. Foto van het fenomeen "tranen van wijn".
Oppervlakteactieve stoffen
De oppervlaktespanning is zichtbaar in andere veel voorkomende verschijnselen, vooral wanneer oppervlakte-actieve stoffen worden gebruikt om de spanning te verlagen:
- Zeepbellen hebben een zeer groot oppervlak met zeer weinig massa. Zeepbellen in zuiver water zijn onstabiel. De toevoeging van oppervlakte-actieve stoffen kan echter een stabiliserend effect hebben op de bellen (zie Marangoni effect). Oppervlakte-actieve stoffen verlagen de oppervlaktespanning van water met een factor drie of meer.
- Emulsies zijn een type oplossing waarbij de oppervlaktespanning een rol speelt. Kleine stukjes olie in zuiver water zullen zich spontaan samenvoegen tot een veel grotere massa. Maar de aanwezigheid van een oppervlakte-actieve stof zorgt voor een vermindering van de oppervlaktespanning, waardoor minuscule oliedruppeltjes in de bulk water stabiel blijven (of omgekeerd).
Basisfysica
Twee definities
Oppervlaktespanning, weergegeven door het symbool γ, wordt gedefinieerd als de kracht langs een lijn van lengte-eenheid, waarbij de kracht evenwijdig is aan het oppervlak maar loodrecht op de lijn staat. Een manier om dit voor te stellen is een vlakke zeepfilm die aan één kant wordt begrensd door een strakke draad met een lengte van L. De draad wordt naar de binnenkant van de film getrokken met een kracht gelijk aan 2 
Een equivalente definitie, die nuttig is in de thermodynamica, is arbeid per oppervlakte-eenheid. Om de oppervlakte van een massa vloeistof met een hoeveelheid, δA, te vergroten, is dus een hoeveelheid arbeid, γ 
De gelijkwaardigheid van de meting van energie per oppervlakte-eenheid aan kracht per lengte-eenheid kan worden aangetoond door dimensionale analyse.
Oppervlakte kromming en druk
Als er geen kracht normaal op een gespannen oppervlak werkt, moet het oppervlak vlak blijven. Maar als de druk aan de ene kant van het oppervlak verschilt van de druk aan de andere kant, resulteert het drukverschil maal de oppervlakte in een normaalkracht. Om ervoor te zorgen dat de oppervlaktespanningskrachten de drukkracht opheffen, moet het oppervlak gekromd zijn. Het diagram toont hoe de kromming van een klein oppervlak leidt tot een netto component van oppervlaktespanningskrachten die normaal op het midden van het oppervlak werken. Wanneer alle krachten in evenwicht zijn, staat de resulterende vergelijking bekend als de vergelijking van Young-Laplace:
waar:
· Δp is het drukverschil.
· 
· Rx en Ry zijn kromtestralen in elk van de assen die evenwijdig zijn aan het oppervlak.
De grootheid tussen haakjes aan de rechterkant is in feite (tweemaal) de gemiddelde kromming van het oppervlak (afhankelijk van de normalisatie).
Oplossingen van deze vergelijking bepalen de vorm van waterdruppels, plassen, menisci, zeepbellen en alle andere vormen die door oppervlaktespanning worden bepaald. (Een ander voorbeeld is de vorm van de indrukken die de voeten van een schaatser maken op het oppervlak van een vijver).
Onderstaande tabel laat zien hoe de interne druk van een waterdruppel toeneemt met afnemende straal. Voor niet al te kleine druppels is het effect subtiel, maar het drukverschil wordt enorm wanneer de druppels de moleculaire grootte benaderen. (In de limiet van een enkel molecuul wordt het begrip zinloos).
| Δp voor waterdruppels met verschillende stralen bij STP | ||||
| Druppelstraal | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Vloeibaar oppervlak
Het is moeilijk om de vorm van het minimale oppervlak dat begrensd wordt door een willekeurig gevormd kader te vinden met alleen wiskunde. Maar door het frame te maken van draad en het in een zeepoplossing te dompelen, verschijnt er binnen enkele seconden een lokaal minimaal oppervlak in de resulterende zeeplaag.
De reden hiervoor is dat het drukverschil over een vloeistofinterface evenredig is met de gemiddelde kromming, zoals blijkt uit de vergelijking van Young-Laplace. Voor een open zeepfilm is het drukverschil nul, dus de gemiddelde kromming is nul, en minimale oppervlakken hebben de eigenschap van een gemiddelde kromming van nul.
Contacthoeken
Het oppervlak van een vloeistof is een interface tussen die vloeistof en een ander medium. De bovenkant van een vijver is bijvoorbeeld een interface tussen het vijverwater en de lucht. Oppervlaktespanning is dus geen eigenschap van de vloeistof alleen, maar een eigenschap van het raakvlak van de vloeistof met een ander medium. Als een vloeistof zich in een vat bevindt, is er naast het raakvlak tussen vloeistof en lucht aan het bovenoppervlak ook een raakvlak tussen de vloeistof en de wanden van het vat. De oppervlaktespanning tussen de vloeistof en de lucht is meestal anders (groter) dan de oppervlaktespanning met de wanden van een vat. Waar de twee oppervlakken elkaar raken, zal de geometrie alle krachten in evenwicht houden.
Waar de twee oppervlakken elkaar ontmoeten, vormen ze een contacthoek, θ 


In het diagram moeten zowel de verticale als de horizontale krachten precies opheffen in het contactpunt, het zogenaamde evenwicht. De horizontale component van 

Het belangrijkste krachtenevenwicht ligt echter in de verticale richting. De verticale component van 

| Vloeistof | Massief | Contacthoek | |||
| water |
| 0° | |||
| diethylether | |||||
| koolstoftetrachloride | |||||
| glycerol | |||||
| azijnzuur | |||||
| water | paraffine | 107° | |||
| zilver | 90° | ||||
| methyljodide | soda lime glas | 29° | |||
| loodglas | 30° | ||||
| gesmolten kwarts | 33° | ||||
| kwik | soda lime glas | 140° | |||
| Enkele contacthoeken tussen vloeistof en vaste stof | |||||
Aangezien de krachten in directe verhouding staan tot hun respectieve oppervlaktespanningen, hebben we ook:
waarbij
· 
· 
· 
· 
Dit betekent dat hoewel het verschil tussen de vloeistof-vaste stof en vaste stof-lucht oppervlaktespanning, γ 


Dit verband bestaat ook in het diagram rechts. Maar in dit geval zien we dat, omdat de contacthoek kleiner is dan 90°, het verschil in oppervlaktespanning tussen vloeistof en vaste stof/lucht negatief moet zijn:
Speciale contacthoeken
Merk op dat in het speciale geval van een water-zilver interface waar de contacthoek gelijk is aan 90°, het verschil in oppervlaktespanning tussen vloeistof en vaste stof/lucht precies nul is.
Een ander speciaal geval is wanneer de contacthoek precies 180° is. Water met speciaal geprepareerd Teflon benadert dit. Een contacthoek van 180° ontstaat wanneer de vloeistof-vaste stof oppervlaktespanning precies gelijk is aan de vloeistof-lucht oppervlaktespanning.
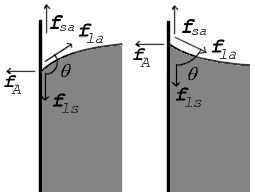
Krachten op het contactpunt getoond voor contacthoek groter dan 90° (links) en kleiner dan 90° (rechts)

Minimaal oppervlak
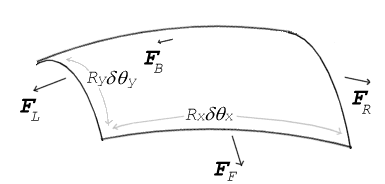
Oppervlaktespanningskrachten die werken op een klein (differentieel) stukje oppervlak. δθx en δθy geven de mate van buiging aan over de afmetingen van het lapje. Het in evenwicht brengen van de trekkrachten met de druk leidt tot de vergelijking van Young-Laplace
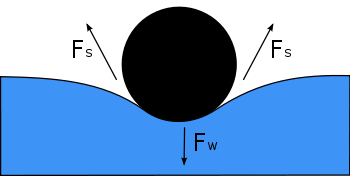
De figuur toont een dwarsdoorsnede van een naald die op het wateroppervlak drijft. Zijn gewicht, Fw , drukt op het oppervlak, en wordt in evenwicht gehouden door de oppervlaktespanningskrachten aan weerszijden, Fs , die elk evenwijdig zijn aan het wateroppervlak op de punten waar ze de naald raken. Merk op dat de horizontale componenten van de twee Fs pijlen in tegengestelde richtingen wijzen, en elkaar dus opheffen, maar dat de verticale componenten in dezelfde richting wijzen en dus optellen om Fw in evenwicht te brengen.
Meetmethoden
Omdat de oppervlaktespanning zich uit in verschillende effecten, zijn er verschillende manieren om deze te meten. Welke methode optimaal is, hangt af van de aard van de te meten vloeistof, de omstandigheden waaronder de spanning moet worden gemeten en de stabiliteit van het oppervlak bij vervorming.
- Du Noüy Ring-methode: De traditionele methode om de oppervlakte- of grensvlakspanning te meten. De bevochtigingseigenschappen van het oppervlak of interface hebben weinig invloed op deze meettechniek. De maximale trekkracht die door het oppervlak op de ring wordt uitgeoefend, wordt gemeten.
- Du Noüy-Padday-methode: Een geminimaliseerde versie van de Du Noüy-methode maakt gebruik van een metalen naald met een kleine diameter in plaats van een ring, in combinatie met een zeer gevoelige microbalans om de maximale trek te registreren. Het voordeel van deze methode is dat zeer kleine monstervolumes (tot enkele tientallen microliters) kunnen worden gemeten met een zeer hoge precisie, zonder dat hoeft te worden gecorrigeerd voor drijfvermogen (voor een naald of liever nog een staaf met de juiste geometrie). Bovendien kan de meting zeer snel worden uitgevoerd, minimaal in ongeveer 20 seconden. De eerste commerciële meerkanaalstrekmeters [CMCeeker] zijn onlangs gebouwd op basis van dit principe.
- Wilhelmy-plaatmethode: Een universele methode die bijzonder geschikt is om de oppervlaktespanning over lange tijdsintervallen te controleren. Een verticale plaat met bekende omtrek wordt op een balans bevestigd en de kracht als gevolg van bevochtiging wordt gemeten.
- Spinnende druppelmethode: Deze techniek is ideaal voor het meten van lage interfaciale spanningen. De diameter van een druppel in een zware fase wordt gemeten terwijl beide worden rondgedraaid.
- Druppelmethode: Met deze techniek kunnen oppervlakte- en grensvlakspanning worden gemeten, zelfs bij hoge temperaturen en drukken. De geometrie van een druppel wordt optisch geanalyseerd. Voor details, zie Druppel.
- Bubbeldrukmethode (methode van Jaeger): Een meettechniek voor het bepalen van de oppervlaktespanning bij korte oppervlakten. De maximale druk van elke bel wordt gemeten.
- Druppelvolumemethode: Een methode voor het bepalen van de interfaciale spanning als functie van de leeftijd van het grensvlak. Vloeistof met een bepaalde dichtheid wordt in een tweede vloeistof met een andere dichtheid gepompt en de tijd tussen de geproduceerde druppels wordt gemeten.
- Capillaire stijgmethode: Het uiteinde van een capillair wordt in de oplossing gedompeld. De hoogte waarop de oplossing in het capillair komt, is gerelateerd aan de oppervlaktespanning door de hieronder besproken vergelijking.
- Stalagmometrische methode: Een methode om een vloeistofdruppel te wegen en af te lezen.
- Sessiele druppelmethode: Een methode om de oppervlaktespanning en dichtheid te bepalen door een druppel op een substraat te plaatsen en de contacthoek te meten (zie Sessile drop technique).
- Trillingsfrequentie van zwevende druppels: De oppervlaktespanning van superfluïde4 He is gemeten door bestudering van de natuurlijke frequentie van trillingsschommelingen van druppels die door magnetisme in de lucht worden gehouden. Deze waarde wordt geschat op 0,375 dyn/cm bij T = 0° K.

De oppervlaktespanning kan worden gemeten met de hangende druppelmethode op een goniometer.
Effecten
Vloeistof in een verticale buis
Een kwikbarometer oude stijl bestaat uit een verticale glazen buis met een diameter van ongeveer 1 cm, gedeeltelijk gevuld met kwik en met een vacuüm (het zogenaamde Torricelli-vacuüm) in het ongevulde volume (zie het diagram rechts). Merk op dat het kwikniveau in het midden van de buis hoger is dan aan de randen, waardoor de bovenkant van het kwik koepelvormig is. Het massamiddelpunt van de hele kwikkolom zou iets lager liggen als de bovenkant van het kwik over de hele doorsnede van de buis vlak zou zijn. Maar de koepelvormige bovenkant geeft iets minder oppervlakte aan de hele kwikmassa. Ook hier geldt dat de twee effecten samen de totale potentiële energie minimaliseren. Een dergelijke oppervlaktevorm staat bekend als een convexe meniscus.
Wij beschouwen de oppervlakte van de hele kwikmassa, inclusief het deel van het oppervlak dat in contact is met het glas, omdat kwik helemaal niet aan glas hecht. De oppervlaktespanning van het kwik werkt dus over het hele oppervlak, ook daar waar het in contact komt met het glas. Als de buis niet uit glas, maar uit koper zou bestaan, zou de situatie heel anders zijn. Kwik hecht zich agressief aan koper. Dus in een koperen buis zal het kwikniveau in het midden van de buis lager zijn dan aan de randen (dat wil zeggen, het zou een holle meniscus zijn). In een situatie waarin de vloeistof aan de wanden van zijn vat kleeft, beschouwen wij het deel van het vloeistofoppervlak dat in contact is met het vat als een vloeistof met een negatieve oppervlaktespanning. De vloeistof probeert dan het contactoppervlak te maximaliseren. In dit geval neemt de potentiële energie dus eerder af dan toe door het contactoppervlak met de tank te vergroten. Die afname is voldoende om de toegenomen potentiële energie te compenseren die gepaard gaat met het optillen van de vloeistof bij de wanden van de container.
Als een buis voldoende smal is en de vloeistof voldoende sterk aan de wanden kleeft, kan de oppervlaktespanning de vloeistof omhoog trekken in de buis, een verschijnsel dat capillaire werking wordt genoemd. De hoogte die de kolom bereikt wordt gegeven door:
waarbij
· 
· 
· 
· 
· 
· 

Plassen op een oppervlak
Het gieten van kwik op een horizontale vlakke glasplaat resulteert in een plas met een voelbare dikte. De plas zal zich slechts verspreiden tot het punt waar hij iets minder dan een halve centimeter dik is, en niet dunner. Ook dit is het gevolg van de sterke oppervlaktespanning van kwik. De vloeistofmassa wordt vlakker omdat daardoor zoveel mogelijk van het kwik naar een zo laag mogelijk niveau wordt gebracht, maar de oppervlaktespanning werkt tegelijkertijd om het totale oppervlak te verkleinen. Het resultaat is het compromis van een plas met een bijna vaste dikte.
Dezelfde oppervlaktespanningsdemonstratie kan worden gedaan met water, kalkwater of zelfs zoutoplossing, maar alleen als de vloeistof niet hecht aan het vlakke oppervlaktemateriaal. Was is zo'n stof. Water dat op een glad, vlak en horizontaal oppervlak van was wordt gegoten, bijvoorbeeld een met was bedekt glasblad, zal zich op dezelfde manier gedragen als kwik dat op glas wordt gegoten.
De dikte van een vloeistofplas op een oppervlak met een contacthoek van 180° wordt gegeven door:
waarbij
|
|
|
|
|
|
|
|
In werkelijkheid zal de dikte van de plassen iets kleiner zijn dan wat met bovenstaande formule wordt voorspeld, omdat slechts weinig oppervlakken een contacthoek van 180° hebben met een vloeistof. Wanneer de contacthoek kleiner is dan 180°, wordt de dikte gegeven door:
Voor kwik op glas is γHg = 487 dyn/cm, ρHg = 13,5 g/cm3 en θ = 140°, wat hHg = 0,36 cm geeft. Voor water op paraffine bij 25 °C is γ = 72 dyn/cm, ρ = 1,0 g/cm3 , en θ = 107°, wat hH2O = 0,44 cm geeft.
De formule voorspelt ook dat wanneer de contacthoek 0° is, de vloeistof zich in een microdunne laag over het oppervlak verspreidt. Van een dergelijk oppervlak wordt gezegd dat het volledig bevochtigbaar is door de vloeistof.
Het uiteenvallen van stromen in druppels
In het dagelijks leven zien we allemaal dat een waterstroom uit een kraan in druppels uiteenvalt, hoe soepel de stroom ook uit de kraan komt. Dit is het gevolg van een verschijnsel dat de Plateau-Rayleigh instabiliteit wordt genoemd en dat volledig voortvloeit uit de effecten van oppervlaktespanning.
De verklaring van deze instabiliteit begint met het bestaan van kleine verstoringen in de stroom. Deze zijn altijd aanwezig, hoe glad de stroom ook is. Als de verstoringen worden opgelost in sinusvormige componenten, blijkt dat sommige componenten toenemen met de tijd, terwijl andere afnemen met de tijd. Van de componenten die met de tijd groeien, groeien sommige sneller dan andere. Of een component afneemt of groeit, en hoe snel hij groeit, is volledig afhankelijk van het golfgetal (een maat voor het aantal pieken en dalen per centimeter) en de straal van de oorspronkelijke cilindrische stroom.
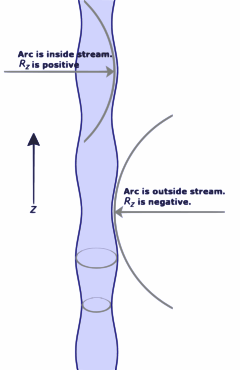
Tussenstadium van een straal die in druppels uiteenvalt. Krommingsstralen in de axiale richting worden getoond. Vergelijking voor de straal van de straal is 





Kleine plasjes water op een glad en schoon oppervlak hebben een voelbare dikte.
Illustratie van hoe een lagere contacthoek leidt tot vermindering van de plasdiepte
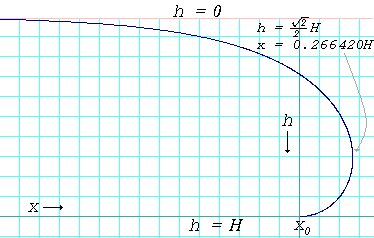
Profielcurve van de rand van een plas waarbij de contacthoek 180° is. De kromme wordt gegeven door de formule 
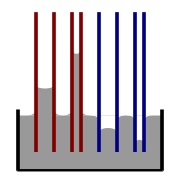
Illustratie van capillaire stijging en daling. Rood=contacthoek kleiner dan 90°; blauw=contacthoek groter dan 90°
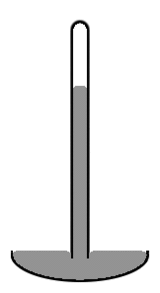
Schema van een kwikbarometer
Gegevenstabel
| Oppervlaktespanning van verschillende vloeistoffen in dyn/cm ten opzichte van lucht | ||
| Vloeistof | Temperatuur °C | Oppervlaktespanning, γ |
| Azijnzuur | 20 | 27.6 |
| Azijnzuur (40,1%) + Water | 30 | 40.68 |
| Azijnzuur (10,0%) + Water | 30 | 54.56 |
| Aceton | 20 | 23.7 |
| Diethylether | 20 | 17.0 |
| Ethanol | 20 | 22.27 |
| Ethanol (40%) + Water | 25 | 29.63 |
| Ethanol (11,1%) + Water | 25 | 46.03 |
| Glycerol | 20 | 63 |
| n-Hexaan | 20 | 18.4 |
| Zoutzuur 17,7M waterige oplossing | 20 | 65.95 |
| Isopropanol | 20 | 21.7 |
| -196 | 8.85 | |
| 15 | 487 | |
| Methanol | 20 | 22.6 |
| n-Octaan | 20 | 21.8 |
| Natriumchloride 6,0M waterige oplossing | 20 | 82.55 |
| Sucrose (55%) + water | 20 | 76.45 |
| Water | 0 | 75.64 |
| Water | 25 | 71.97 |
| Water | 50 | 67.91 |
| Water | 100 | 58.85 |
Galerij van effecten
· 
Het breken van een bewegend wateroppervlak dat op een lepel stuitert.
· 
Foto van stromend water dat zich vasthecht aan een hand. De oppervlaktespanning creëert het vel water tussen de stroom en de hand.
· 
Een zeepbel balanceert oppervlaktespanningskrachten tegen interne pneumatische druk.
· 
Oppervlaktespanning voorkomt dat een munt zinkt: de munt is onbetwistbaar dichter dan water, dus moet hij een volume verplaatsen dat groter is dan zijn eigen volume, wil de opwaartse druk de massa in evenwicht houden.
· 
Een madeliefje. De hele bloem ligt onder het niveau van het (ongestoorde) vrije oppervlak. Het water stijgt soepel op rond de rand. De oppervlaktespanning voorkomt dat het water de lucht tussen de bloemblaadjes vult en de bloem mogelijk onderdompelt.
· 
Een metalen paperclip drijft op water. Meestal kunnen er voorzichtig meerdere worden toegevoegd zonder dat het water overloopt.
· .jpg)
Een aluminium munt drijft op het wateroppervlak bij 10 °C. Bij elk extra gewicht zou de munt naar de bodem zakken.
Vragen en antwoorden
V: Wat is oppervlaktespanning?
A: Oppervlaktespanning is een effect waarbij het oppervlak van een vloeistof sterk is en een gewicht kan vasthouden. Het zorgt ervoor dat sommige kleine dingen op het oppervlak kunnen drijven, ook al zouden ze dat normaal niet kunnen, en dat sommige insecten (bv. schaatsenrijders) op het wateroppervlak kunnen lopen.
V: Wat veroorzaakt oppervlaktespanning?
A: Oppervlaktespanning wordt veroorzaakt doordat de moleculen in de vloeistof elkaar aantrekken (cohesie).
V: Wat zijn de afmetingen van oppervlaktespanning?
A: Oppervlaktespanning heeft de dimensie van kracht per lengte-eenheid, of van energie per oppervlakte-eenheid. De twee zijn gelijkwaardig, maar wanneer men het heeft over energie per oppervlakte-eenheid, gebruikt men de term oppervlakte-energie - een meer algemene term in die zin dat hij ook van toepassing is op vaste stoffen en niet alleen op vloeistoffen.
V: Hoe beïnvloedt oppervlaktespanning de materiaalkunde?
A: In de materiaalkunde wordt oppervlaktespanning gebruikt voor ofwel oppervlaktespanning ofwel vrije oppervlakte-energie.
V: Hoe draagt cohesie bij tot de oppervlaktespanning?
A: Cohesie draagt bij tot oppervlaktespanning doordat moleculen in een vloeistof door elkaar worden aangetrokken, waardoor aan het oppervlak een sterke binding ontstaat die gewicht kan houden en bepaalde voorwerpen of wezens (bv. schaatsenrijders) in staat stelt er anders mee om te gaan dan anders het geval zou zijn.
V: Waarin verschilt deze eigenschap van andere eigenschappen van vloeistoffen?
A: Deze eigenschap verschilt van andere eigenschappen van vloeistoffen omdat ze van invloed is op de interactie tussen voorwerpen en het oppervlak ervan, en niet zozeer in het oppervlak of door hun gedrag in het algemeen.
Zoek in de encyclopedie